Question 1
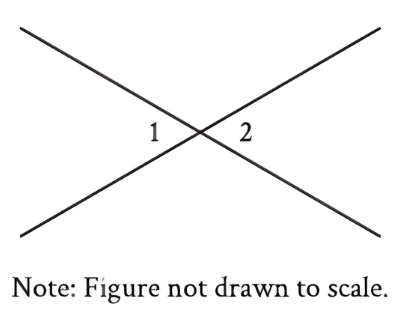
In the figure, two lines intersect at a point. Angle `1` and angle `2` are vertical angles. The measure of angle `1` is `72^circ`. What is the measure of angle `2`?
A) `72^circ`
B) `108^circ`
C) `144^circ`
D) `288^circ`
Mark as Complete
Mark Scheme
Question 2
In triangle `ABC`, the measure of angle `B` is `52^circ` and the measure of angle `C` is `17^circ`. What is the measure of angle `A`?
A) `21^circ`
B) `35^\circ`
C) `69^circ`
D) `111^circ`
Mark as Complete
Mark Scheme
Question 3
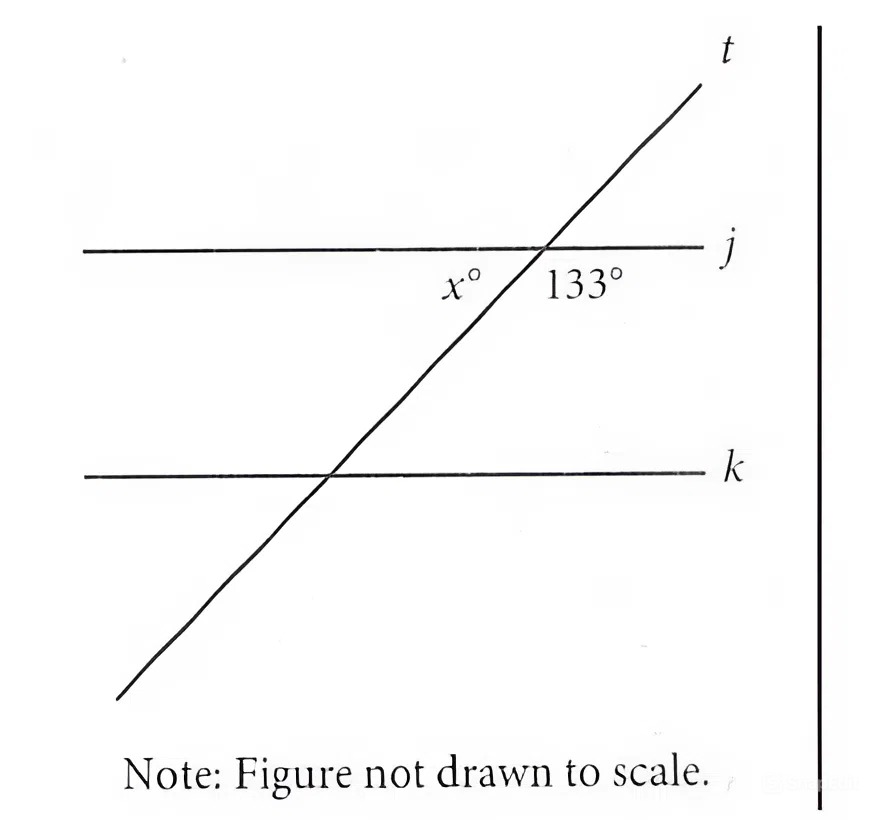 In the figure, line `j` is parallel to line `k`. What is the value of `x`?
In the figure, line `j` is parallel to line `k`. What is the value of `x`?
Mark as Complete
Mark Scheme
Question 4
In triangle `JKL`, `\cos(K) = 24/51` and `angle J` is a right angle. What is the value of `\cos(L)`?
Mark as Complete
Mark Scheme
Question 5
In triangle `ABC`, angle `B` is a right angle. The length of side `AB` is `10√37` and the length of side `BC` is `24√37`. What is the length of side `AC`?
A) `14√37`
B) `26√37`
C) `34√37`
D) `√34xx37`.
Mark as Complete
Mark Scheme
Question 6
`RS = 440`
`ST = 384`
`TR = 584`
The side lengths of right triangle `RST` are given. Triangle `RST` is similar to triangle `UVW`, where `S` corresponds to `V` and `T` corresponds to `W`. What is the value of `tan W`?
A) `48/73`
B) `55/73`
C) `48/55`
D) `55/48`
Mark as Complete
Mark Scheme
Question 7
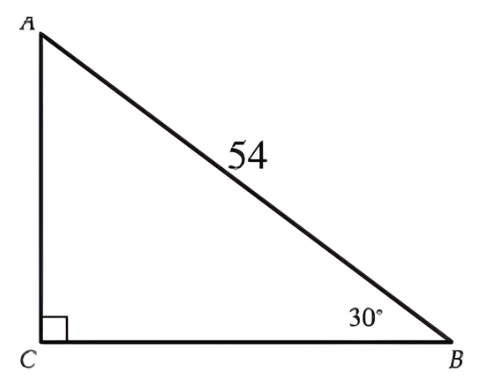
Right triangle `ABC` is shown. What is the value of `tan A`?
A) `√3 / 54`
B) `1 / √3`
C) `√3`
D) `27√3`
Mark as Complete
Mark Scheme
Question 8
In right triangle `ABC`, angle `C` is the right angle and `BC` = 162. Point `D` on side `AB` is connected by a line segment with point `E` on side `AC` such that line segment `DE` is parallel to side `BC` and `CE` = `2AE`. What is the length of line segment `DE`?
Mark as Complete
Mark Scheme
Question 1

In the figure, two lines intersect at a point. Angle `1` and angle `2` are vertical angles. The measure of angle `1` is `72^circ`. What is the measure of angle `2`?
A) `72^circ`
B) `108^circ`
C) `144^circ`
D) `288^circ`
Answer: A
Vertical angles are the angles opposite each other when two lines cross. They are always equal. Since the measure of angle `1` is `72^circ`, the measure of angle `2` is also `72^circ`.
Question 2
In triangle `ABC`, the measure of angle `B` is `52^circ` and the measure of angle `C` is `17^circ`. What is the measure of angle `A`?
A) `21^circ`
B) `35^\circ`
C) `69^circ`
D) `111^circ`
Answer: D
The sum of the angle measures of a triangle is `180^circ`. Adding the measures of angles `B` and `C` gives `52^circ + 17^circ = 69^circ`. Therefore, the measure of angle `A` is `180 - 69 = 111^circ`.
Question 3
 In the figure, line `j` is parallel to line `k`. What is the value of `x`?
In the figure, line `j` is parallel to line `k`. What is the value of `x`?
Answer: `47`
Based on the figure, the angle with measure `x^circ` and the angle with measure `133^circ` together form a straight line. Therefore, these two angles are supplementary, so the sum of their measures is `180^circ`. It follows that `x + 133 = 180`. Subtracting `133` from both sides of this equation yields `x = 47`.
Question 4
In triangle `JKL`, `\cos(K) = 24/51` and `angle J` is a right angle. What is the value of `\cos(L)`?
Answer: `15/17` or `0.882`
It's given that `angle J` is the right angle in triangle `JKL`. The cosine of an acute angle in a right triangle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. It’s given that `cos(K)=24/51`. This can be written as `cos(K) = 8/17`.
Since the cosine of `angle K` is a ratio, it follows that the length of the side adjacent to `angle K` is `8n` and the length of the hypotenuse is `17n`, where `n` is a constant. Therefore, `JK = 8n` and `KL = 17n`.
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. For triangle `JKL`, it follows that `(JL)^2+(JK)^2= (KL)^2`. Substituting `8n` for `JK` and `17n` for `KL` yields `(JL)^2+(8n)^2 = (17n)^2`, which is equivalent to `(JL)^2+64n^2 = 289n^2`.
Subtracting`64n^2` from each side of this equation yields `(JL)^2= 225n^2`. Taking the square root of each side of this equation yields `JL= 15n`. Since `cos(L)={JL}/{KL}`, it follows that `cos(L)= {15n}/{17n}`, which can be rewritten as `cos(L)= 15/17`.
Question 5
In triangle `ABC`, angle `B` is a right angle. The length of side `AB` is `10√37` and the length of side `BC` is `24√37`. What is the length of side `AC`?
A) `14√37`
B) `26√37`
C) `34√37`
D) `√34xx37`.
Answer: B
Use the Pythagorean theorem, `a² + b² = c²`, where `a` and `b` are the legs and `c` is the hypotenuse (side `AC`).
`(10√37)² + (24√37)² = c²`
`100(37) + 576(37) = c²`
`676(37) = c²`
Taking the square root of both sides gives `c = √676 xx √37`, which is `26√37`. The length of side `AC` is `26√37`.
Question 6
`RS = 440`
`ST = 384`
`TR = 584`
The side lengths of right triangle `RST` are given. Triangle `RST` is similar to triangle `UVW`, where `S` corresponds to `V` and `T` corresponds to `W`. What is the value of `tan W`?
A) `48/73`
B) `55/73`
C) `48/55`
D) `55/48`
Answer: D
We start with the following observation: the hypotenuse of triangle `RST` is the longest side and is across from the right angle. The longest side length given is `584`, which is the length of side `TR`. Therefore, the hypotenuse of triangle `RST` is side `TR`, and the right angle is angle `S`. Since triangle `RST` is similar to triangle `UVW`, where `S` corresponds to `V` and `T` corresponds to `W`, the right angle of triangle `UVW` is angle `V`, and the hypotenuse of triangle `UVW` is side `WU`.
Recall that the tangent of an acute angle in a right triangle is the ratio of the length of the opposite side, which is the side across from the angle, to the length of the adjacent side, which is the side closest to the angle that is not the hypotenuse. Since the opposite side of angle `W` is `UV` and the adjacent side of `W` is `VW`, we have `tan W = (UV)/(VW)`. Since the lengths of corresponding sides of similar triangles are proportional,`(RS)/(UV) = (ST)/(VW)` This implies that `(UV)/(VW) = (RS)/(ST)`. It follows that `tan W = (UV)/(VW)` is equivalent to `tan W = (RS)/(ST)`. Substituting `440` for `RS` and `384` for `ST` in this equation yields `tan W = 440/384`, or `tan W = 55/48`.
Question 7

Right triangle `ABC` is shown. What is the value of `tan A`?
A) `√3 / 54`
B) `1 / √3`
C) `√3`
D) `27√3`
Answer: C
The triangle is a right triangle with a `30^circ` angle at `B`. This means it is a 30-60-90 triangle, and angle `A` must be `60^circ`. In a 30-60-90 triangle, the side lengths are in the ratio `x` (opposite `30^circ`), `x√3` (opposite `60^circ`), and `2x` (hypotenuse).
The hypotenuse is `54`, so `2x = 54` and `x = 27`. The side opposite angle `A` (leg `BC`) is `x√3 = 27√3` and the side adjacent to angle `A` (leg `AC`) is `x = 27`. The tangent of an angle is `(opposite)/(adjacent)`. Therefore, `tan(A) = (27√3) / 27`, which simplifies to `√3`.
Question 8
In right triangle `ABC`, angle `C` is the right angle and `BC` = 162. Point `D` on side `AB` is connected by a line segment with point `E` on side `AC` such that line segment `DE` is parallel to side `BC` and `CE` = `2AE`. What is the length of line segment `DE`?
Answer: `54`
Since `DE` is parallel to `BC`, triangle `ADE` is similar to triangle `ABC`. This means the ratio of corresponding sides is equal: `(DE)/(BC) = (AE)/(AC)`.
We are given `CE = 2AE`, so the full length of side `AC = AE + CE = AE + 2AE = 3AE`.
Now substitute the known values into the proportion: `(DE) / 162 = (AE) / (3AE)`.
The `AE` terms cancel out, leaving `(DE) / 162 = 1/3`. Multiply both sides by `162` to find `DE = 54`.
Question 1

In the figure, two lines intersect at a point. Angle `1` and angle `2` are vertical angles. The measure of angle `1` is `72^circ`. What is the measure of angle `2`?
A) `72^circ`
B) `108^circ`
C) `144^circ`
D) `288^circ`
Question 2
In triangle `ABC`, the measure of angle `B` is `52^circ` and the measure of angle `C` is `17^circ`. What is the measure of angle `A`?
A) `21^circ`
B) `35^\circ`
C) `69^circ`
D) `111^circ`
Question 3
 In the figure, line `j` is parallel to line `k`. What is the value of `x`?
In the figure, line `j` is parallel to line `k`. What is the value of `x`?
Question 4
In triangle `JKL`, `\cos(K) = 24/51` and `angle J` is a right angle. What is the value of `\cos(L)`?
Question 5
In triangle `ABC`, angle `B` is a right angle. The length of side `AB` is `10√37` and the length of side `BC` is `24√37`. What is the length of side `AC`?
A) `14√37`
B) `26√37`
C) `34√37`
D) `√34xx37`.
Question 6
`RS = 440`
`ST = 384`
`TR = 584`
The side lengths of right triangle `RST` are given. Triangle `RST` is similar to triangle `UVW`, where `S` corresponds to `V` and `T` corresponds to `W`. What is the value of `tan W`?
A) `48/73`
B) `55/73`
C) `48/55`
D) `55/48`
Question 7

Right triangle `ABC` is shown. What is the value of `tan A`?
A) `√3 / 54`
B) `1 / √3`
C) `√3`
D) `27√3`
Question 8
In right triangle `ABC`, angle `C` is the right angle and `BC` = 162. Point `D` on side `AB` is connected by a line segment with point `E` on side `AC` such that line segment `DE` is parallel to side `BC` and `CE` = `2AE`. What is the length of line segment `DE`?