Question 1
What is the area of a rectangle with a length of `17` centimeters (cm) and a width of `7` cm?
A) `24` `text{cm}^2`
B) `48` `text{cm}^2`
C) `119` `text{cm}^2`
D) `576` `text{cm}^2`
Mark as Complete
Mark Scheme
Question 2
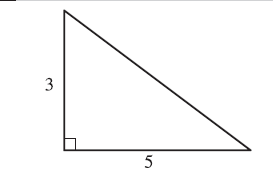
The figure shows the lengths, in inches, of two sides of a right triangle. What is the area of the triangle, in square inches?
Mark as Complete
Mark Scheme
Question 3
A right circular cylinder has a volume of `432` cubic centimeters. The area of the base of the cylinder is `24` square centimeters. What is the height, in centimeters, of the cylinder?
A) `18`
B) `24`
C) `216`
D) `10,368`
Mark as Complete
Mark Scheme
Question 4
A cylinder has a diameter of `8` inches and a height of `12` inches. What is the volume, in cubic inches, of the cylinder?
A) `16\pi`
B) `96\pi`
C) `192\pi`
D) `768\pi`
Mark as Complete
Mark Scheme
Question 1
What is the area of a rectangle with a length of `17` centimeters (cm) and a width of `7` cm?
A) `24` `text{cm}^2`
B) `48` `text{cm}^2`
C) `119` `text{cm}^2`
D) `576` `text{cm}^2`
Answer: C
The area of a rectangle with length `l` and width `w` can be found using the formula `A = lw`. It is given that the rectangle has a length of `17` cm and a width of `7` cm. Therefore, the area of this rectangle is`A = 17(7)`, or `119` `text{cm}^2`.
Question 2

The figure shows the lengths, in inches, of two sides of a right triangle. What is the area of the triangle, in square inches?
Answer: `15/2` or `7.5`
The area of a triangle is given by the formula `A = 1/2 xx base xx height`. For the given right triangle, the base is `5` inches and the height is `3` inches. So, the area is `A = 1/2 xx (5) xx (3)`, which equals `15/2` or `7.5` square inches.
Question 3
A right circular cylinder has a volume of `432` cubic centimeters. The area of the base of the cylinder is `24` square centimeters. What is the height, in centimeters, of the cylinder?
A) `18`
B) `24`
C) `216`
D) `10,368`
Answer: A
The formula for the volume of a cylinder is `V""= "Area of base" xx h`.
We are given `"V" = 432` and `"Area of base" = 24`. Substituting these values into the formula gives `432 = 24 xx h`.
To solve for the height `h`, divide both sides by `24`: `h = 432 / 24 = 18`.
The height is `18` centimeters.
Question 4
A cylinder has a diameter of `8` inches and a height of `12` inches. What is the volume, in cubic inches, of the cylinder?
A) `16\pi`
B) `96\pi`
C) `192\pi`
D) `768\pi`
Answer: C
The base of a cylinder is a circle with a diameter equal to the diameter of the cylinder. The volume, `V`, of a cylinder can be found by multiplying the area of the circular base, `A`, by the height of the cylinder, `h`, or `V= Ah`. The area of a circle can be found using the formula `A= pi r^2`, where `r` is the radius of the circle. It is given that the diameter of the cylinder is `8` inches. Thus, the radius of this circular base is `4` inches. Therefore, the area of the circular base of the cylinder is `A = pi(4)^2`, or `16pi` square inches. It’s given that the height of the cylinder is `12` inches. Substituting `16pi` for `A` and `12` for `h` in the formula `V = Ah` gives `V= 16pi(12)`, or `192pi` cubic inches.
Question 1
What is the area of a rectangle with a length of `17` centimeters (cm) and a width of `7` cm?
A) `24` `text{cm}^2`
B) `48` `text{cm}^2`
C) `119` `text{cm}^2`
D) `576` `text{cm}^2`
Question 2

The figure shows the lengths, in inches, of two sides of a right triangle. What is the area of the triangle, in square inches?
Question 3
A right circular cylinder has a volume of `432` cubic centimeters. The area of the base of the cylinder is `24` square centimeters. What is the height, in centimeters, of the cylinder?
A) `18`
B) `24`
C) `216`
D) `10,368`
Question 4
A cylinder has a diameter of `8` inches and a height of `12` inches. What is the volume, in cubic inches, of the cylinder?
A) `16\pi`
B) `96\pi`
C) `192\pi`
D) `768\pi`