Question 1
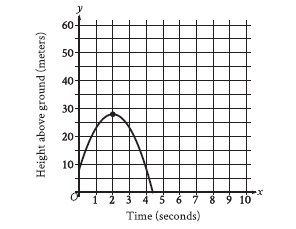
An object was launched upward from a platform. The graph shown models the height above ground, `y`, in meters, of the object `x` seconds after it was launched. For which of the following intervals of time was the height of the object increasing for the entire interval?
A) From `x=0` to `x=2`
B) From `x=0` to`x=4`
C) From `x=2` to `x=3`
D) From `x=3`to `x=4`
Mark as Complete
Mark Scheme
Question 2
`P(t) = "1,800"(1.02)^t`
The function `P` gives the estimated number of marine mammals in a certain area, where `t` is the number of years since a study began. What is the best interpretation of `P(0) = "1,800"` in this context?
A) The estimated number of marine mammals in the area was `102` when the study began.
B) The estimated number of marine mammals in the area was `"1,800"` when the study began.
C) The estimated number of marine mammals in the area increased by `102` each year during the study.
D) The estimated number of marine mammals in the area increased by `"1,800"` each year during the study.
Mark as Complete
Mark Scheme
Question 3
The function `f` is defined by `f(x) = x^3 + 9`. What is the value of `f(2)`?
A) `14`
B) `15`
C) `17`
D) `18`
Mark as Complete
Mark Scheme
Question 4
The function `h` is defined by `h(x) = 8 / (5x + 6)`. What is the value of `h(2)`?
Mark as Complete
Mark Scheme
Question 5
| Time (years) | Total amount (dollars) |
| `0` | `604.00` |
| `1` | `604.42` |
| `2` | `608.84` |
Rosa opened a savings account at a bank. The table shows the exponential relationship between the time `t`, in years, since Rosa opened the account and the total amount `n`, in dollars, in the account. If Rosa made no additional deposits or withdrawals, which of the following equations best represents the relationship between `t` and `n`?
A) `n = (1 + 604)^t`
B) `n = (1 + 0.004)^t`
C) `n = 604(1 + 0.004)^t`
D) `n = 0.004(1 + 604)^t`
Mark as Complete
Mark Scheme
Question 6
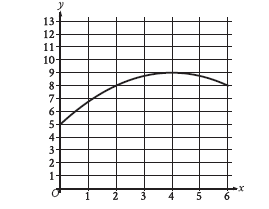
The graph models the number of active projects a company was working on `x` months after the end of November 2012, where `0 ≤ x ≤ 6`. According to the model, what is the predicted number of active projects the company was working on at the end of November 2012?
A) `0`
B) `5`
C) `8`
D) `9`
Mark as Complete
Mark Scheme
Question 7
An object is kicked from a platform. The equation `h = -4.9t^2 + 7t + 9` represents this situation, where `h` is the height of the object above the ground, in meters, `t` seconds after it is kicked. Which number represents the height, in meters, from which the object was kicked?
A) `0`
B) `4.9`
C) `7`
D) `9`
Mark as Complete
Mark Scheme
Question 8
`h(x) = x^2 - 3`
Which table gives three values of `x` and their corresponding values of `h(x)` for the given function `h`?
A)
| `x` | `1` | `2` | `3` |
| `h(x)` | `4` | `5` | `6` |
B)
| `x` | `1` | `2` | `3` |
| `h(x)` | `-2` | `1` | `6` |
C)
| `x` | `1` | `2` | `3` |
| `h(x)` | `-1` | `1` | `3` |
D)
| `x` | `1` | `2` | `3` |
| `h(x)` | `-2` | `1` | `3` |
Mark as Complete
Mark Scheme
Question 9
`f(x) = 4x^2 - 50x + 126`
The given equation defines the function `f`. For what value of `x` does `f(x)` reach its minimum?
Mark as Complete
Mark Scheme
Question 10
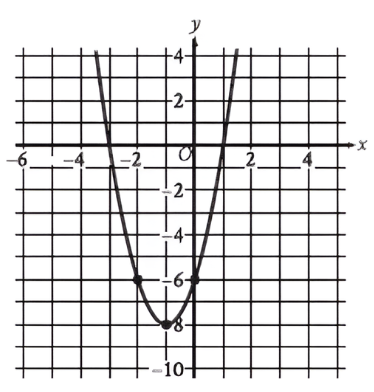
The graph of `y = 2x² + bx + c` is shown, where `b` and `c` are constants. What is the value of `bc`?
Mark as Complete
Mark Scheme
Question 11
`f(x) = (1.84)^(x/4)`
The function `f` is defined by the given equation. The equation can be rewritten as `f(x) = (1 + p/100)^x` where `p` is a constant. Which of the following is closest to the value of `p`?
A) `16`
B) `21`
C) `46`
D) `96`
Mark as Complete
Mark Scheme
Question 12
The function `f` is defined by `f(x) = asqrt((x + b))`, where `a` and `b` are constants. In the `xy`-plane, the graph of `y = f(x)` passes through the point `(-24, 0)`, and `f(24) < 0`. Which of the following must be true?
A) `f(0) = 24`
B) `f(0) = -24`
C) `a > b`
D) `a < b`
Mark as Complete
Mark Scheme
Question 13
At the time that an article was first featured on the home page of a news website, there were `40` comments on the article. An exponential model estimates that at the end of each hour after the article was first featured on the home page, the number of comments on the article had increased by `190%` of the number of comments on the article at the end of the previous hour. Which of the following equations best represents this model, where `C` is the estimated number of comments on the article `t` hours after the article was first featured on the home page and `t ≤ 4`?
A) `C = 40(1.19)^t`
B) `C = 40(1.9)^t`
C) `C = 40(19)^t`
D) `C = 40(2.9)^t`
Mark as Complete
Mark Scheme
Question 1

An object was launched upward from a platform. The graph shown models the height above ground, `y`, in meters, of the object `x` seconds after it was launched. For which of the following intervals of time was the height of the object increasing for the entire interval?
A) From `x=0` to `x=2`
B) From `x=0` to`x=4`
C) From `x=2` to `x=3`
D) From `x=3`to `x=4`
Answer: A
The graph shows the height of the object increasing from the start at `x=0` until it reaches its peak at `x=2` seconds. After `x=2`, the height begins to decrease. Therefore, the height was increasing over the entire interval from `x=0` to `x=2`.
Question 2
`P(t) = "1,800"(1.02)^t`
The function `P` gives the estimated number of marine mammals in a certain area, where `t` is the number of years since a study began. What is the best interpretation of `P(0) = "1,800"` in this context?
A) The estimated number of marine mammals in the area was `102` when the study began.
B) The estimated number of marine mammals in the area was `"1,800"` when the study began.
C) The estimated number of marine mammals in the area increased by `102` each year during the study.
D) The estimated number of marine mammals in the area increased by `"1,800"` each year during the study.
Answer: B
The input `t=0` represents `0` years since the study began—in other words, the moment the study began. The output `P(0)` gives the number of marine mammals at that time. Therefore, `P(0) = "1,800"` means the estimated number of marine mammals was `"1,800"` when the study began. The input `t=0` represents `0` years since the study began—in other words, the moment the study began. The output `P(0)` gives the number of marine mammals at that time. Therefore, `P(0) = "1,800"` means the estimated number of marine mammals was `"1,800"` when the study began.
Question 3
The function `f` is defined by `f(x) = x^3 + 9`. What is the value of `f(2)`?
A) `14`
B) `15`
C) `17`
D) `18`
Answer: C
Substituting `2` for `x` in the equation `f(x) = x^3 + 9` yields `f(2) = (2)^3 + 9`. This is equivalent to `f(2) = 8 + 9`, or `f(2) = 17`.
Question 4
The function `h` is defined by `h(x) = 8 / (5x + 6)`. What is the value of `h(2)`?
Answer: `1/2` or `0.5`
To find `h(2)`, substitute `2` for `x` in the function: `h(2) = 8 / (5(2) + 6)`. This simplifies to `h(2) = 8 / (10 + 6)`, which is `8 / 16` or `1/2`.
Question 5
| Time (years) | Total amount (dollars) |
| `0` | `604.00` |
| `1` | `604.42` |
| `2` | `608.84` |
Rosa opened a savings account at a bank. The table shows the exponential relationship between the time `t`, in years, since Rosa opened the account and the total amount `n`, in dollars, in the account. If Rosa made no additional deposits or withdrawals, which of the following equations best represents the relationship between `t` and `n`?
A) `n = (1 + 604)^t`
B) `n = (1 + 0.004)^t`
C) `n = 604(1 + 0.004)^t`
D) `n = 0.004(1 + 604)^t`
Answer: C
It is given that the relationship between `t` and `n` is exponential. Since the value of `n` increases as the value of `t` increases, the relationship between `t` and `n` can be represented by an increasing exponential equation of the form `n = a(1 + b)^t`, where `a` and `b` are positive constants.
The table shows that when `t = 0`, `n = 604`. Substituting `0` for `t` and `604` for `n` in the equation `n = a(1 + b)^t` yields `604 = a(1 + b)^0`, which is equivalent to `604 = a(1)`, or `604 = a`. Substituting `604` for `a` in the equation `n = a(1 + b)^t` yields `n = 604(1 + b)^t`.
The table also shows that when `t = 1`, `n = 606.42`. Substituting `1` for `t` and `606.42` for `n` in the new equation `n = 604(1 + b)^t` yields , or `606.42 = 604(1 + b)`. Dividing both sides of this equation by `604` yields approximately `1.004 = 1 + b`. Subtracting `1` from both sides of this equation yields that the value of `b` is approximately `0.004`. Substituting `0.004` for `b` in the equation `n = 604(1 + b)^t` yields `n = 604(1 + 0.004)^t`.
Therefore, of the choices, choice C best represents the relationship between `t` and `n`.
Question 6

The graph models the number of active projects a company was working on `x` months after the end of November 2012, where `0 ≤ x ≤ 6`. According to the model, what is the predicted number of active projects the company was working on at the end of November 2012?
A) `0`
B) `5`
C) `8`
D) `9`
Answer: B
"At the end of November 2012" corresponds to `x = 0` months after that date. The value of the model at `x = 0` is the `y`-intercept. Looking at the graph, the `y`-intercept is at the point `(0, 5)`. Therefore, the predicted number of active projects was `5`.
Question 7
An object is kicked from a platform. The equation `h = -4.9t^2 + 7t + 9` represents this situation, where `h` is the height of the object above the ground, in meters, `t` seconds after it is kicked. Which number represents the height, in meters, from which the object was kicked?
A) `0`
B) `4.9`
C) `7`
D) `9`
Answer: D
It is given that the equation `h = -4.9t^2 + 7t + 9` represents this situation, where `h` is the height, in meters, of the object `t` seconds after it is kicked. It follows that the height, in meters, from which the object was kicked is the value of `h` when `t = 0`. Substituting `0` for `t` in the equation `h = -4.9t^2 + 7t + 9` yields `h = -4.9(0)^2 + 7(0) + 9`, or `h = 9`. Therefore, the object was kicked from a height of `9` meters.
Question 8
`h(x) = x^2 - 3`
Which table gives three values of `x` and their corresponding values of `h(x)` for the given function `h`?
A)
| `x` | `1` | `2` | `3` |
| `h(x)` | `4` | `5` | `6` |
B)
| `x` | `1` | `2` | `3` |
| `h(x)` | `-2` | `1` | `6` |
C)
| `x` | `1` | `2` | `3` |
| `h(x)` | `-1` | `1` | `3` |
D)
| `x` | `1` | `2` | `3` |
| `h(x)` | `-2` | `1` | `3` |
Answer: B
Substituting `1` for `x` in the equation `h(x) = x^2 - 3` yields `h(1) = (1)^2 - 3`, or`h(1) = -2`.
Substituting `2` for `x` in the equation `h(x) = x^2 - 3` yields `h(2) = (2)^2 -`3, or `h(2) = 1`.
Finally, substituting `3` for `x` in the equation `h(x) = x^2 - 3` yields `h(3) = (3)^2 - 3`, or `h(3) = 6`.
Therefore, `h(x)` is `-2` when `x` is `1`, `h(x)` is `1` when `x` is `2`, and `h(x)` is `6` when `x` is `3`.
Choice B is a table with these values of `x` and their corresponding values of `h(x)`.
Question 9
`f(x) = 4x^2 - 50x + 126`
The given equation defines the function `f`. For what value of `x` does `f(x)` reach its minimum?
Answer: `25/4` or `6.25`
The given equation can be rewritten in the form `f(x)= a(x - h)^2 + k`, where `a`, `h`, and `k` are constants. When `a > 0`, `h` is the value of `x` for which `f(x)` reaches its minimum since `(x - h)^2 >= 0`, for all `x`. The given equation can be rewritten as `f(x)= 4x^2 - 50x + 126`, which is equivalent to
`f(x)= 4 ( x^2 - 50/4 x ) + 126 = 4 ( x^2 - 25/2 x) + 126`.
This can be rewritten as `f(x) = 4 [( x - 25/4)^2 - 121/4] + 126`, which is equivalent to
`f(x)= 4 ( x - 25/4 )^2 - 121 + 126 = 4(x - 25/4)^2 + 5`.
Therefore, `h= 25/4` and the value of `x` for which `f(x)` reaches its minimum is `25/4` (or, equivalently, `6.25`).
Question 10

The graph of `y = 2x² + bx + c` is shown, where `b` and `c` are constants. What is the value of `bc`?
Answer:`-24`
The graph passes through the point `(0, -6)`, which is the y-intercept.
By substituting `x=0` and `y=-6` into the equation, we find that `c = -6`. The graph also passes through the vertex at `(-1, -8)`.
Substitute `x=-1`, `y=-8`, and `c=-6` into the equation: `-8 = 2(-1)² + b(-1) - 6`. This simplifies to`-8 = 2 - b - 6`, or `-8 = -4 - b`, which gives `b = 4`.
The value of bc is `(4)(-6) = -24`.
Question 11
`f(x) = (1.84)^(x/4)`
The function `f` is defined by the given equation. The equation can be rewritten as `f(x) = (1 + p/100)^x` where `p` is a constant. Which of the following is closest to the value of `p`?
A) `16`
B) `21`
C) `46`
D) `96`
Answer: A
Rewrite the function using exponent rules:`f(x) = (1.84)^(x/4) = (1.84^(1/4))^x`. Calculate the value of `1.84^(1/4)`, which is approximately `1.16467`. So, `f(x) ≈ (1.16467)^x`.
Comparing this to `f(x) = (1 + p/100)^x`, we see that `1 + p/100 ≈ 1.16467`. This means `p/100 ≈ 0.16467`, so`p ≈ 16.467`. The closest choice is `16`.
Question 12
The function `f` is defined by `f(x) = asqrt((x + b))`, where `a` and `b` are constants. In the `xy`-plane, the graph of `y = f(x)` passes through the point `(-24, 0)`, and `f(24) < 0`. Which of the following must be true?
A) `f(0) = 24`
B) `f(0) = -24`
C) `a > b`
D) `a < b`
Answer: D
The function is `f(x) = asqrt((x + b))`.
From the point `(-24, 0)`, substituting `x=-24` and `f(x)=0` gives `0 = a√(-24 + b)`.
Since`f(24) < 0`, '`a`' cannot be `0`, so `-24 + b` must be `0`, which means `b = 24`.
Now the function is `f(x) = asqrt(x + 24)`.
The condition`f(24) < 0` implies `asqrt(24 + 24) < 0`, or `asqrt(48 < 0`. Since √48 is positive, '`a`' must be negative `(a < 0)`.
Given `a <`0 and `b = 24`, we evaluate the options. Options A and B are incorrect as `f(0) = asqrt24`, which must be negative. Option C (`a > b`) is false because a negative 'a' cannot be greater than positive `24`. Option D `(a < b)` is true because any negative 'a' is always less than positive `24`.
Question 13
At the time that an article was first featured on the home page of a news website, there were `40` comments on the article. An exponential model estimates that at the end of each hour after the article was first featured on the home page, the number of comments on the article had increased by `190%` of the number of comments on the article at the end of the previous hour. Which of the following equations best represents this model, where `C` is the estimated number of comments on the article `t` hours after the article was first featured on the home page and `t ≤ 4`?
A) `C = 40(1.19)^t`
B) `C = 40(1.9)^t`
C) `C = 40(19)^t`
D) `C = 40(2.9)^t`
Answer: D
The initial number of comments is `40`. An increase of `190%` means that each hour, the number of comments is multiplied by `1 + 1.90 = 2.9`. Therefore, the exponential model is `C = 40(2.9)^t`.
Question 1

An object was launched upward from a platform. The graph shown models the height above ground, `y`, in meters, of the object `x` seconds after it was launched. For which of the following intervals of time was the height of the object increasing for the entire interval?
A) From `x=0` to `x=2`
B) From `x=0` to`x=4`
C) From `x=2` to `x=3`
D) From `x=3`to `x=4`
Question 2
`P(t) = "1,800"(1.02)^t`
The function `P` gives the estimated number of marine mammals in a certain area, where `t` is the number of years since a study began. What is the best interpretation of `P(0) = "1,800"` in this context?
A) The estimated number of marine mammals in the area was `102` when the study began.
B) The estimated number of marine mammals in the area was `"1,800"` when the study began.
C) The estimated number of marine mammals in the area increased by `102` each year during the study.
D) The estimated number of marine mammals in the area increased by `"1,800"` each year during the study.
Question 3
The function `f` is defined by `f(x) = x^3 + 9`. What is the value of `f(2)`?
A) `14`
B) `15`
C) `17`
D) `18`
Question 4
The function `h` is defined by `h(x) = 8 / (5x + 6)`. What is the value of `h(2)`?
Question 5
| Time (years) | Total amount (dollars) |
| `0` | `604.00` |
| `1` | `604.42` |
| `2` | `608.84` |
Rosa opened a savings account at a bank. The table shows the exponential relationship between the time `t`, in years, since Rosa opened the account and the total amount `n`, in dollars, in the account. If Rosa made no additional deposits or withdrawals, which of the following equations best represents the relationship between `t` and `n`?
A) `n = (1 + 604)^t`
B) `n = (1 + 0.004)^t`
C) `n = 604(1 + 0.004)^t`
D) `n = 0.004(1 + 604)^t`
Question 6

The graph models the number of active projects a company was working on `x` months after the end of November 2012, where `0 ≤ x ≤ 6`. According to the model, what is the predicted number of active projects the company was working on at the end of November 2012?
A) `0`
B) `5`
C) `8`
D) `9`
Question 7
An object is kicked from a platform. The equation `h = -4.9t^2 + 7t + 9` represents this situation, where `h` is the height of the object above the ground, in meters, `t` seconds after it is kicked. Which number represents the height, in meters, from which the object was kicked?
A) `0`
B) `4.9`
C) `7`
D) `9`
Question 8
`h(x) = x^2 - 3`
Which table gives three values of `x` and their corresponding values of `h(x)` for the given function `h`?
A)
| `x` | `1` | `2` | `3` |
| `h(x)` | `4` | `5` | `6` |
B)
| `x` | `1` | `2` | `3` |
| `h(x)` | `-2` | `1` | `6` |
C)
| `x` | `1` | `2` | `3` |
| `h(x)` | `-1` | `1` | `3` |
D)
| `x` | `1` | `2` | `3` |
| `h(x)` | `-2` | `1` | `3` |
Question 9
`f(x) = 4x^2 - 50x + 126`
The given equation defines the function `f`. For what value of `x` does `f(x)` reach its minimum?
Question 10

The graph of `y = 2x² + bx + c` is shown, where `b` and `c` are constants. What is the value of `bc`?
Question 11
`f(x) = (1.84)^(x/4)`
The function `f` is defined by the given equation. The equation can be rewritten as `f(x) = (1 + p/100)^x` where `p` is a constant. Which of the following is closest to the value of `p`?
A) `16`
B) `21`
C) `46`
D) `96`
Question 12
The function `f` is defined by `f(x) = asqrt((x + b))`, where `a` and `b` are constants. In the `xy`-plane, the graph of `y = f(x)` passes through the point `(-24, 0)`, and `f(24) < 0`. Which of the following must be true?
A) `f(0) = 24`
B) `f(0) = -24`
C) `a > b`
D) `a < b`
Question 13
At the time that an article was first featured on the home page of a news website, there were `40` comments on the article. An exponential model estimates that at the end of each hour after the article was first featured on the home page, the number of comments on the article had increased by `190%` of the number of comments on the article at the end of the previous hour. Which of the following equations best represents this model, where `C` is the estimated number of comments on the article `t` hours after the article was first featured on the home page and `t ≤ 4`?
A) `C = 40(1.19)^t`
B) `C = 40(1.9)^t`
C) `C = 40(19)^t`
D) `C = 40(2.9)^t`