Question 1
Jay walks at a speed of `3` miles per hour and runs at a speed of `5` miles per hour. He walks for `w` hours and runs for `r` hours for a combined total of `14` miles. Which equation represents this situation?
A) `3w + 5r = 14`
B) `1/3w + 1/5r = 14`
C) `1/3w + 1/5r = 112`
D) `3w + 5r = 112`
Mark as Complete
Mark Scheme
Question 2
The number `y` is `84` less than the number `x`. Which equation represents the relationship between `x` and `y`?
A) `y = x + 84`
B) `y = x/84`
C) `y = 84x`
D) `y = x - 84`
Mark as Complete
Mark Scheme
Question 3
The graph of `7x + 2y = -31` in the `xy`-plane has an `x`-intercept at `(a, 0)` and a `y`-intercept at `(0, b)`, where `a` and `b` are constants. What is the value of `b/a`?
A) `-7/2`
B) `-2/7`
C) `2/7`
D) `7/2`
Mark as Complete
Mark Scheme
Question 4
`5G+45R = 380`
At a school fair, students can win colored tokens that are worth a different number of points depending on the color. One student won `G` green tokens and `R` red tokens worth a total of `380` points. The given equation represents this situation. How many more points is a red token worth than a green token?
Mark as Complete
Mark Scheme
Question 5
An object travels at a constant speed of `12` centimeters per second. At this speed, what is the time, in seconds, that it would take for the object to travel `108` centimeters?
A) `9`
B) `96`
C) `120`
D) `972`
Mark as Complete
Mark Scheme
Question 6
John paid a total of `$165` for a microscope by making a down payment of `$37` plus `p` monthly payments of `$16` each. Which of the following equations represents this situation?
A) `16p - 37 = 165`
B) `37p - 16 = 165`
C) `16p + 37 = 165`
D) `37p + 16 = 165`
Mark as Complete
Mark Scheme
Question 7
| `x` | `y` |
| `0` | `18` |
| `1` | `13` |
| `2` | `8` |
The table shows three values of `x` and their corresponding values of `y`. There is a linear relationship between `x` and `y`. Which of the following equations represents this relationship?
A) `y = 18x + 13`
B) `y = 18x + 18`
C) `y = -5x + 13`
D) `y = -5x + 18`
Mark as Complete
Mark Scheme
Question 8
Line `k` is defined by `y = 7x + 1/8`. Line `j` is perpendicular to line `k` in the `xy`-plane. What is the slope of line `j`?
A) `-8`
B) `-1/7`
C) `1/8`
D) `7`
Mark as Complete
Mark Scheme
Question 9
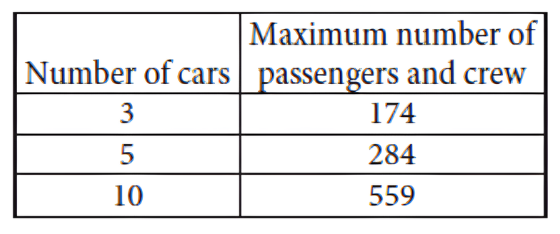 The table shows the linear relationship between the number of cars, `c`, on a commuter train and the maximum number of passengers and crew, `p`, that the train can carry. Which equation represents the linear relationship between `c` and `p`?
The table shows the linear relationship between the number of cars, `c`, on a commuter train and the maximum number of passengers and crew, `p`, that the train can carry. Which equation represents the linear relationship between `c` and `p`?
A) `55c − p = −9`
B) `55c − p = 9`
C) `55p − c = −9`
D) `55p − c = 9`
Mark as Complete
Mark Scheme
Question 10
What is the `y`-coordinate of the `y`-intercept of the graph of `3x/7 = -5y/9 + 21` in the `xy`-plane?
Mark as Complete
Mark Scheme
Question 11
In the `xy`-plane, line `l` passes through the point `(0, 0)` and is parallel to the line represented by the equation `y= 8x + 2`. If line `l` also passes through the point `(3, d)`, what is the value of `d`?
Mark as Complete
Mark Scheme
Question 12
`14j + 5k = m`
The given equation relates the numbers `j`, `k`, and `m`. Which equation correctly expresses `k` in terms of `j` and `m`?
A) `k = (m - 14j)/5`
B) `k = m/5 - 14j`
C) `k = (14j - m)/5`
D) `k = 5m - 14j`
Mark as Complete
Mark Scheme
Question 1
Jay walks at a speed of `3` miles per hour and runs at a speed of `5` miles per hour. He walks for `w` hours and runs for `r` hours for a combined total of `14` miles. Which equation represents this situation?
A) `3w + 5r = 14`
B) `1/3w + 1/5r = 14`
C) `1/3w + 1/5r = 112`
D) `3w + 5r = 112`
Answer: A
Jay walks at a speed of `3` miles per hour for `w` hours, so Jay walks a total of `3w` miles. On the other hand, since Jay runs at a speed of `5` miles per hour for `r` hours, Jay runs a total of `5r` miles. Therefore, the total number of miles Jay travels can be represented by `3w + 5r`. Since the combined total number of miles is `14`, the equation `3w + 5r = 14` represents this situation.
Question 2
The number `y` is `84` less than the number `x`. Which equation represents the relationship between `x` and `y`?
A) `y = x + 84`
B) `y = x/84`
C) `y = 84x`
D) `y = x - 84`
Answer: D
It is given that the number `y` is `84` less than the number `x`. A number that is `84` less than the number `x` is equivalent to `84` subtracted from the number `x`, or `x - 84`. Therefore, the equation `y = x - 84` represents the relationship between `x` and `y`.
Question 3
The graph of `7x + 2y = -31` in the `xy`-plane has an `x`-intercept at `(a, 0)` and a `y`-intercept at `(0, b)`, where `a` and `b` are constants. What is the value of `b/a`?
A) `-7/2`
B) `-2/7`
C) `2/7`
D) `7/2`
Answer: D
The `x`-coordinate a of the `x`-intercept `(a, 0)` can be found by substituting `0` for `y` in the given equation, which gives `7x + 2(0) = -31`, or `7x = -31`. Dividing both sides of this equation by `7` yields `x = -31/7`. Therefore, the value of `a` is `-31/7`. The `y`-coordinate `b` of the `y`-intercept `(0, b)` can be found by substituting `0` for `x` in the given equation, which gives `7(0) + 2y = -31`, or `2y = -31`. Dividing both sides of this equation by `2` yields `y = -31/2`. Therefore, the value of `b` is `-31/2`. It follows that the value of `b/a` is `(-31/2) / (-31/7)`, which is equivalent to `7/2`, or `3.5`.
Question 4
`5G+45R = 380`
At a school fair, students can win colored tokens that are worth a different number of points depending on the color. One student won `G` green tokens and `R` red tokens worth a total of `380` points. The given equation represents this situation. How many more points is a red token worth than a green token?
Answer: 40
It’s given that `5G + 45R = 380`, where `G` is the number of green tokens and `R` is the number of red tokens won by one student and these tokens were worth a total of `380` points. Since the equation represents the situation where the student won points with green tokens and red tokens for a total of `380` points, the number of points that each red token is worth is represented by the coefficient of `R`, and the number of points each green token is worth is represented by the coefficient of `G`. The difference between the two is `45 - 5 = 40`. Therefore, a red token is worth `40` more points than a green token.
Question 5
An object travels at a constant speed of `12` centimeters per second. At this speed, what is the time, in seconds, that it would take for the object to travel `108` centimeters?
A) `9`
B) `96`
C) `120`
D) `972`
Answer: A
If the object travels `108` centimeters at a speed of `12` centimeters per second, then the relationship between the distance travelled and time can be represented by the equation `s = 12t`. Here, `s` is the distance, in centimeters, travelled by the object in `t` seconds. To find the time it would take for the object to travel `108` centimeters, we set `s = 108` to obtain the equation `108 = 12t`. Dividing both sides of this equation by `12` yields `t = 9`. Thus, it takes `9` seconds for the object to travel `108` centimeters.
Question 6
John paid a total of `$165` for a microscope by making a down payment of `$37` plus `p` monthly payments of `$16` each. Which of the following equations represents this situation?
A) `16p - 37 = 165`
B) `37p - 16 = 165`
C) `16p + 37 = 165`
D) `37p + 16 = 165`
Answer: C
It is given that John made a `$16` payment each month for `p` months. The total amount of these payments can be represented by the expression `16p`. The down payment can be added to that amount to find the total amount John paid, yielding the expression `16p + 37`. It is also given that John paid a total of `$165`. Therefore, the expression for the total amount John paid can be set equal to that amount, yielding the equation `16p + 37 = 165`.
Question 7
| `x` | `y` |
| `0` | `18` |
| `1` | `13` |
| `2` | `8` |
The table shows three values of `x` and their corresponding values of `y`. There is a linear relationship between `x` and `y`. Which of the following equations represents this relationship?
A) `y = 18x + 13`
B) `y = 18x + 18`
C) `y = -5x + 13`
D) `y = -5x + 18`
Answer: D
A linear relationship can be represented by an equation of the form `y = mx + b`, where `m` and `b` are constants. It is given in the table that when `x = 0`, `y = 18`. Substituting `0` for `x` and `18` for `y` in `y = mx + b` yields `18 = m(0) + b`, or `18 = b`. Substituting `18` for `b` in the equation `y = mx + b` yields `y = mx + 18`. It's also given in the table that when `x = 1`, `y = 13`. Substituting `1` for `x` and `13` for `y` in the equation `y = mx + 18` yields `13 = m(1) + 18`, or `13 = m + 18`. Subtracting `18` from both sides of this equation yields `-5 = m`. Therefore, the equation `y = -5x + 18` represents the relationship between `x` and `y`.
Question 8
Line `k` is defined by `y = 7x + 1/8`. Line `j` is perpendicular to line `k` in the `xy`-plane. What is the slope of line `j`?
A) `-8`
B) `-1/7`
C) `1/8`
D) `7`
Answer: B
The slope of line `k` is `7`. The slopes of perpendicular lines are opposite reciprocals of each other. The opposite reciprocal of `7` is `-1/7`. Therefore, the slope of line `j` is `-1/7`.
Question 9
 The table shows the linear relationship between the number of cars, `c`, on a commuter train and the maximum number of passengers and crew, `p`, that the train can carry. Which equation represents the linear relationship between `c` and `p`?
The table shows the linear relationship between the number of cars, `c`, on a commuter train and the maximum number of passengers and crew, `p`, that the train can carry. Which equation represents the linear relationship between `c` and `p`?
A) `55c − p = −9`
B) `55c − p = 9`
C) `55p − c = −9`
D) `55p − c = 9`
Answer: A
First, find the slope (rate of change) using two points from the table, such as (3, 174) and (5, 284):
`m = (284 - 174) / (5 - 3) = 110 / 2 = 55`
The equation is `p = 55c + b`. Use a point, like (3, 174), to find `b`:
`174 = 55(3) + b`
so `174 = 165 + b`
which means `b = 9`. The equation is `p = 55c + 9`. Rearranging this into the form given in the options gives `55c - p = -9`.
Question 10
What is the `y`-coordinate of the `y`-intercept of the graph of `3x/7 = -5y/9 + 21` in the `xy`-plane?
Answer: `189/5` or `37.8`
The `y`-intercept occurs where `x=0`. Substitute `x=0` into the equation: `3(0)/7 = -5y/9 + 21`, which simplifies to `0 = -5y/9 + 21`. Subtract `21` from both sides: `-21 = -5y/9`. Multiply both sides by `9`: `-189 = -5y`. Finally, divide by `-5` to get `y = 189/5`.
Question 11
In the `xy`-plane, line `l` passes through the point `(0, 0)` and is parallel to the line represented by the equation `y= 8x + 2`. If line `l` also passes through the point `(3, d)`, what is the value of `d`?
Answer: `24`
A line in the `xy`-plane can be defined by the equation `y=mx+b`, where `m` is the slope of the line and `b` is the `y`-coordinate of the `y`-intercept of the line. It’s given that line `l` passes through the point `(0, 0)`. Therefore, the `y`-coordinate of the `y`-intercept of line `l` is `0`. It is given that line l is parallel to the line represented by the equation `y = 8x + 2`. Since parallel lines have the same slope, it follows that the slope of line `l` is `8`. Therefore, line `l` can be represented by the equation `y=8x+0`, or simply `y = 8x`. If line `l` also passes through the point `(3, d)`, then `d = 8(3) = 24`.
Question 12
`14j + 5k = m`
The given equation relates the numbers `j`, `k`, and `m`. Which equation correctly expresses `k` in terms of `j` and `m`?
A) `k = (m - 14j)/5`
B) `k = m/5 - 14j`
C) `k = (14j - m)/5`
D) `k = 5m - 14j`
Answer: A
Subtracting `14j` from each side of the given equation results in `5k = m - 14j`. Dividing each side of this equation by `5` results in `k = (m - 14j)/5`.
Question 1
Jay walks at a speed of `3` miles per hour and runs at a speed of `5` miles per hour. He walks for `w` hours and runs for `r` hours for a combined total of `14` miles. Which equation represents this situation?
A) `3w + 5r = 14`
B) `1/3w + 1/5r = 14`
C) `1/3w + 1/5r = 112`
D) `3w + 5r = 112`
Question 2
The number `y` is `84` less than the number `x`. Which equation represents the relationship between `x` and `y`?
A) `y = x + 84`
B) `y = x/84`
C) `y = 84x`
D) `y = x - 84`
Question 3
The graph of `7x + 2y = -31` in the `xy`-plane has an `x`-intercept at `(a, 0)` and a `y`-intercept at `(0, b)`, where `a` and `b` are constants. What is the value of `b/a`?
A) `-7/2`
B) `-2/7`
C) `2/7`
D) `7/2`
Question 4
`5G+45R = 380`
At a school fair, students can win colored tokens that are worth a different number of points depending on the color. One student won `G` green tokens and `R` red tokens worth a total of `380` points. The given equation represents this situation. How many more points is a red token worth than a green token?
Question 5
An object travels at a constant speed of `12` centimeters per second. At this speed, what is the time, in seconds, that it would take for the object to travel `108` centimeters?
A) `9`
B) `96`
C) `120`
D) `972`
Question 6
John paid a total of `$165` for a microscope by making a down payment of `$37` plus `p` monthly payments of `$16` each. Which of the following equations represents this situation?
A) `16p - 37 = 165`
B) `37p - 16 = 165`
C) `16p + 37 = 165`
D) `37p + 16 = 165`
Question 7
| `x` | `y` |
| `0` | `18` |
| `1` | `13` |
| `2` | `8` |
The table shows three values of `x` and their corresponding values of `y`. There is a linear relationship between `x` and `y`. Which of the following equations represents this relationship?
A) `y = 18x + 13`
B) `y = 18x + 18`
C) `y = -5x + 13`
D) `y = -5x + 18`
Question 8
Line `k` is defined by `y = 7x + 1/8`. Line `j` is perpendicular to line `k` in the `xy`-plane. What is the slope of line `j`?
A) `-8`
B) `-1/7`
C) `1/8`
D) `7`
Question 9
 The table shows the linear relationship between the number of cars, `c`, on a commuter train and the maximum number of passengers and crew, `p`, that the train can carry. Which equation represents the linear relationship between `c` and `p`?
The table shows the linear relationship between the number of cars, `c`, on a commuter train and the maximum number of passengers and crew, `p`, that the train can carry. Which equation represents the linear relationship between `c` and `p`?
A) `55c − p = −9`
B) `55c − p = 9`
C) `55p − c = −9`
D) `55p − c = 9`
Question 10
What is the `y`-coordinate of the `y`-intercept of the graph of `3x/7 = -5y/9 + 21` in the `xy`-plane?
Question 11
In the `xy`-plane, line `l` passes through the point `(0, 0)` and is parallel to the line represented by the equation `y= 8x + 2`. If line `l` also passes through the point `(3, d)`, what is the value of `d`?
Question 12
`14j + 5k = m`
The given equation relates the numbers `j`, `k`, and `m`. Which equation correctly expresses `k` in terms of `j` and `m`?
A) `k = (m - 14j)/5`
B) `k = m/5 - 14j`
C) `k = (14j - m)/5`
D) `k = 5m - 14j`