Question 1
Kirchhoff’s first law is a consequence of the conservation of which physical quantity?
A. Charge.
B. Energy.
C. Linear momentum.
D. Potential difference.
Easy
Mark as Complete
Mark Scheme
Question 2
Three resistors, R1, R2 and R3, are connected in parallel to a cell. The currents in the resistors are I1, I2 and I3. The potential differences across the resistors are V1, V2 and V3. The current in the cell is I0. The potential difference across the cell is V0, as shown.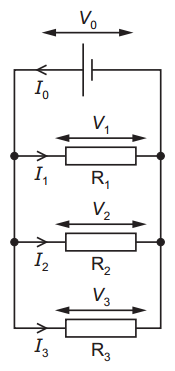 Which equation can be obtained by applying Kirchhoff’s second law to the circuit?
Which equation can be obtained by applying Kirchhoff’s second law to the circuit?
A. I0 = I1 = I2 = I3
B. I0 = I1 + I2 + I3
C. V0 = V1 = V2 = V3
D. V0 = V1 + V2 + V3
Medium
Mark as Complete
Mark Scheme
Question 3
Kirchhoff’s first and second laws are a consequence of the conservation of which quantities?
A. Charge and energy.
B. Charge and resistance.
C. Mass and energy.
D. Mass and resistance.
Easy
Mark as Complete
Mark Scheme
Question 4
The circuit shown contains three cells of electromotive forces 3.0 V, 2.0 V and 4.0 V, in series with a resistor of resistance 5.0 `Omega`. The cells have negligible internal resistance.
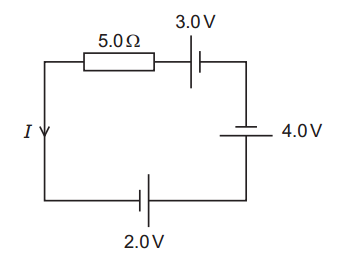 What is the current I in the circuit?
What is the current I in the circuit?
A. 0.20 A.
B. 0.60 A.
C. 1.0 A.
D. 1.8 A.
Medium
Mark as Complete
Mark Scheme
Question 5
Four identical resistors are connected in a circuit, as shown.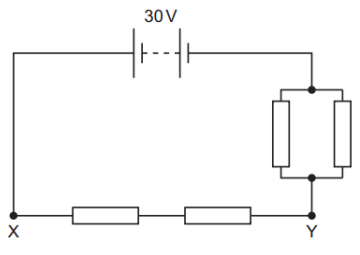 The battery has negligible internal resistance and an e.m.f. of 30 V.
The battery has negligible internal resistance and an e.m.f. of 30 V.
What is the potential difference between the two points X and Y?
Medium
Mark as Complete
Mark Scheme
Question 6
A battery of negligible internal resistance is connected to three resistors, as shown.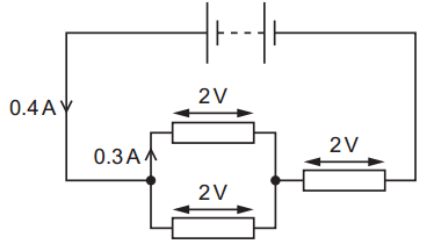 The potential difference across each resistor is 2 V.
The potential difference across each resistor is 2 V.
The current from the battery is 0.4 A and the current through one of the resistors connected in parallel is 0.3 A.
What is the current through the other resistor connected in parallel and what is the electromotive force (e.m.f.) of the battery?
| current/A | e.m.f./V | |
|---|---|---|
| A | 0.1 | 4 |
| B | 0.3 | 4 |
| C | 0.1 | 6 |
| D | 0.3 | 6 |
Medium
Mark as Complete
Mark Scheme
Question 7
Two cells of e.m.f. E1 and E2 and negligible internal resistance are connected into the network as shown.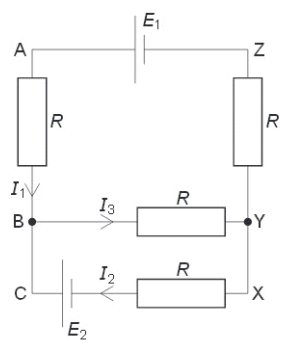 Use Kirchhoff’s laws to state the relation:
Use Kirchhoff’s laws to state the relation:
a. Between currents I1, I2, and I3.
c. Between E1, E2, , I1 and I2 in loop ABCXYZA.
Medium
Mark as Complete
Mark Scheme
Question 8
The diagram shows a circuit in which the battery has negligible internal resistance.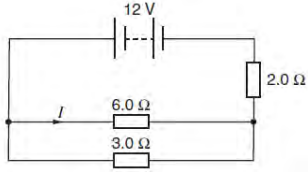 What is the value of the current I ?
What is the value of the current I ?
A. 1.0 A.
B. 1.6 A.
C. 2.0 A.
D. 3.0 A.
Medium
Mark as Complete
Mark Scheme
Question 9
A cell, two resistors of equal resistance and an ammeter are used to construct four circuits. The resistors are the only parts of the circuits that have resistance. In which circuit will the ammeter show the greatest reading?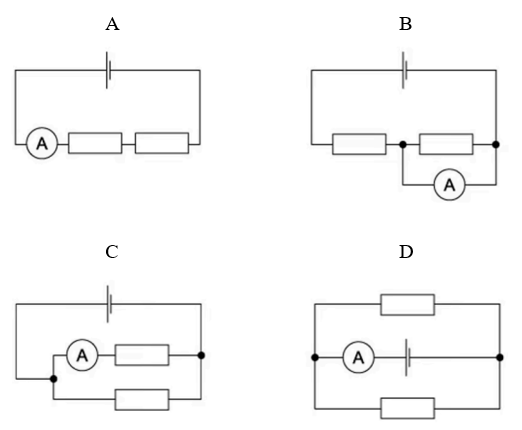
Medium
Mark as Complete
Mark Scheme
Question 10
When four identical resistors are connected as shown in diagram 1, the ammeter reads 1.0 A, and the voltmeter reads zero. 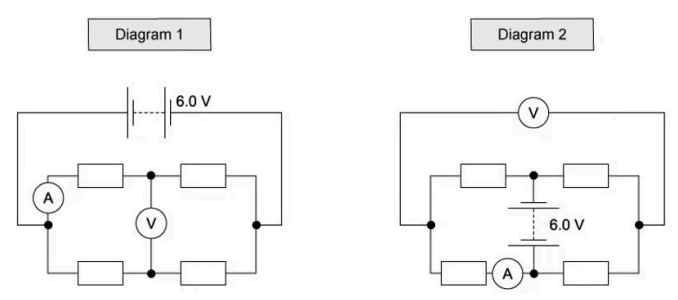 The resistors and meters are reconnected to the supply, as shown in diagram 2.
The resistors and meters are reconnected to the supply, as shown in diagram 2.
What are the meter readings in diagram 2?
| Voltmeter reading/V | Ammeter reading/A | |
|---|---|---|
| A | 0.0 | 1.0 |
| B | 3.0 | 0.5 |
| C | 3.0 | 1.0 |
| D | 6.0 | 0.0 |
Hard
Mark as Complete
Mark Scheme
Question 1
Kirchhoff’s first law is a consequence of the conservation of which physical quantity?
A. Charge.
B. Energy.
C. Linear momentum.
D. Potential difference.
Answer: A
A. Correct:
Kirchhoff’s first law - also called the junction rule - states that:
The total current entering a junction equals the total current leaving the junction.
Current is the flow of electric charge, so this law reflects the conservation of electric charge. It implies that charge cannot accumulate at a junction - it must flow continuously, and the amount going in must equal the amount going out.
B. Incorrect: This relates to Kirchhoff’s second law, not the first.
C. Incorrect: Linear momentum is a concept from mechanics, not circuit theory.
D. Incorrect: Potential difference (voltage) is not conserved — it drops across components.
Question 2
Three resistors, R1, R2 and R3, are connected in parallel to a cell. The currents in the resistors are I1, I2 and I3. The potential differences across the resistors are V1, V2 and V3. The current in the cell is I0. The potential difference across the cell is V0, as shown. Which equation can be obtained by applying Kirchhoff’s second law to the circuit?
Which equation can be obtained by applying Kirchhoff’s second law to the circuit?
A. I0 = I1 = I2 = I3
B. I0 = I1 + I2 + I3
C. V0 = V1 = V2 = V3
D. V0 = V1 + V2 + V3
Answer: C
A. Incorrect: In parallel, current splits between branches. So the individual branch currents are not equal.
B. Incorrect: This is correct, but it follows from Kirchhoff’s first Llaw, not the second law.
C. Correct:
Kirchhoff’s second law (loop rule): The sum of the potential differences (voltage gains and drops) around any closed loop is zero.
So, in each closed loop that includes the cell and one resistor branch, the total voltage drop across the resistor must equal the battery voltage.
In a parallel circuit, each resistor is connected directly across the battery, so: V0 = V1 = V2 = V3.
D. Incorrect: In parallel, each branch has the same voltage, not additive voltages.
Question 3
Kirchhoff’s first and second laws are a consequence of the conservation of which quantities?
A. Charge and energy.
B. Charge and resistance.
C. Mass and energy.
D. Mass and resistance.
Answer: A
A. Correct:
Kirchhoff’s first law (junction rule):
The total current entering a junction equals the total current leaving it.
This law is a direct result of the conservation of electric charge. Charge cannot accumulate at a junction - it must be conserved in any electrical pathway.
B. Incorrect:
Resistance is not a conserved quantity.
It's a property of materials/components, not something that adds up or stays constant in a loop or junction.
C. Incorrect:
While energy conservation is correct, mass is not involved in electric circuit behavior.
Electric current is due to movement of charges, not the conservation of physical mass.
D. Incorrect: Both mass and resistance are irrelevant together in this context.
Question 4
The circuit shown contains three cells of electromotive forces 3.0 V, 2.0 V and 4.0 V, in series with a resistor of resistance 5.0 `Omega`. The cells have negligible internal resistance.
 What is the current I in the circuit?
What is the current I in the circuit?
A. 0.20 A.
B. 0.60 A.
C. 1.0 A.
D. 1.8 A.
From the diagram:
3.0 V are aligned with current (positive).
2.0 V is aligned against the current (negative).
Net e.m.f = 3.0 + 4.0 − 2.0 = 5.0 V
Current: `I=E/R=5/5="1 A"`
Question 5
Four identical resistors are connected in a circuit, as shown. The battery has negligible internal resistance and an e.m.f. of 30 V.
The battery has negligible internal resistance and an e.m.f. of 30 V.
What is the potential difference between the two points X and Y?
Current flow: `I=30/(2.5R)`.
Potential difference between X and Y:
`V_(XY)=Ixx2R=30/(2.5R)xx2R="24 V"`.
Question 6
A battery of negligible internal resistance is connected to three resistors, as shown. The potential difference across each resistor is 2 V.
The potential difference across each resistor is 2 V.
The current from the battery is 0.4 A and the current through one of the resistors connected in parallel is 0.3 A.
What is the current through the other resistor connected in parallel and what is the electromotive force (e.m.f.) of the battery?
| current/A | e.m.f./V | |
|---|---|---|
| A | 0.1 | 4 |
| B | 0.3 | 4 |
| C | 0.1 | 6 |
| D | 0.3 | 6 |
Answer: A
From Kirchhoff’s current law (current conservation), the total current from the battery goes through:
One series resistor (on top).
Then splits into two parallel resistors.
So `I_("total") =I_("series") =I_("parallel1") +I_("parallel2") ⇒0.4=0.3+I_P ⇒I_P ="0.1 A"`
Each resistor has a voltage of 2 V across it.
The total voltage across the battery is the sum of voltages across the resistors in the series path from + to − terminal:
Top series resistor: 2 V.
Bottom parallel path: also 2 V (same for both).
`"e.m.f." = 2 V "(top)" + 2 V"(bottom)" = "4 V"`.
Question 7
Two cells of e.m.f. E1 and E2 and negligible internal resistance are connected into the network as shown. Use Kirchhoff’s laws to state the relation:
Use Kirchhoff’s laws to state the relation:
a. Between currents I1, I2, and I3.
c. Between E1, E2, , I1 and I2 in loop ABCXYZA.
a. At junction B, the current I3 splits into I1 and I2. So by Kirchhoff’s first law:
I1 + I2 = I3
Pass through:
E.m.f. source E2 (from C to B, gaining potential).
Resistor with I2 from X to C → drop of I2R
Resistor with I3 from Y to B → drop of I3R
Apply the loop rule: E2 = I3R + I2R
c. Path: A → B → C → X → Y → Z → A
Pass through:
Two resistors with I1 (AZ and AB): drop of 2I1R
One resistor with I2: drop of I2R
E.m.f. gain from E1, loss from E2
Apply the loop rule:
E1 − E2 = 2I1R − I2R
Question 8
The diagram shows a circuit in which the battery has negligible internal resistance. What is the value of the current I ?
What is the value of the current I ?
A. 1.0 A.
B. 1.6 A.
C. 2.0 A.
D. 3.0 A.
Answer: D
`R_(6Omega)` and `R_(6Omega)` are connected in parallel.
`1/R_(||) = 1/6 + 1/3 = 3/6 => R_(||) = 2 " " Omega`
`R_(||)` and `R_(2Omega)` and are connected in series.
`R_("total") = R_(||) + 2 = 2 + 2 = 4 " "Omega`
Using Ohm's law: `I = V/R = 12/4 = "3 A"`
Question 9
A cell, two resistors of equal resistance and an ammeter are used to construct four circuits. The resistors are the only parts of the circuits that have resistance. In which circuit will the ammeter show the greatest reading?
Answer: D
A. Incorrect: Circuit is in a series arrangement, the current will be the lower than in a parallel arrangement.
`R_T = R + R = 2R`, so the current is `I = E / (2R)`
B. Incorrect: Circuit is in a series arrangement, the current will be the lower than in a parallel arrangement.
`R_T = R + 0 = R`, so the curent is `I = E / R`
C. Incorrect: Current splits at a junction, so, the ammeter gives only half the total current in the circuit.
D. Correct:
2 resistors are in a parallel combination, so the combined resistance is
`1 / R_T = 1 / R + 1 / R = 2 / R`, therefore, `R_T = R / 2`
The current in circuit is `I = E / (R / 2) = (2E) / R`
This is the same current as circuit C, however, at a junction, the current splits.
In this D, the ammeter is connected directly to the positive terminal, so it reads the value of the current flowing in the whole circuit, whereas the current in C will read half the total current.
Therefore, the ammeter in circuit D will have the greatest reading.
Question 10
When four identical resistors are connected as shown in diagram 1, the ammeter reads 1.0 A, and the voltmeter reads zero.  The resistors and meters are reconnected to the supply, as shown in diagram 2.
The resistors and meters are reconnected to the supply, as shown in diagram 2.
What are the meter readings in diagram 2?
| Voltmeter reading/V | Ammeter reading/A | |
|---|---|---|
| A | 0.0 | 1.0 |
| B | 3.0 | 0.5 |
| C | 3.0 | 1.0 |
| D | 6.0 | 0.0 |
Answer: A
In diagram 1, the voltmeter reads zero because the potential difference across it is zero, meaning that both of its junctions are at the same potential.
From Kirchhoff's first law, current splits at a junction.
Since the resistors are identical, the current splits equally into the two branches.
The ammeter reads a current of 1.0 A, so the total current in the circuit is 1.0 + 1.0 = 2.0 A.
In diagram 2, current flows from the positive terminal of the supply and is split equally at a junction, so, the ammeter still reads the current that has been split equally into two.
This current is equal to `2.0/2="1.0 A"`
From the junction connected to the positive terminal of the supply, the current splits at the bottom junction and rejoins again at the top junction to return to the negative terminal.
Since the same amount of current flows through identical resistors the potential of the left and right junctions would be the same.
Therefore, the potential difference across the voltmeter is zero.
Question 1
Kirchhoff’s first law is a consequence of the conservation of which physical quantity?
A. Charge.
B. Energy.
C. Linear momentum.
D. Potential difference.
Question 2
Three resistors, R1, R2 and R3, are connected in parallel to a cell. The currents in the resistors are I1, I2 and I3. The potential differences across the resistors are V1, V2 and V3. The current in the cell is I0. The potential difference across the cell is V0, as shown. Which equation can be obtained by applying Kirchhoff’s second law to the circuit?
Which equation can be obtained by applying Kirchhoff’s second law to the circuit?
A. I0 = I1 = I2 = I3
B. I0 = I1 + I2 + I3
C. V0 = V1 = V2 = V3
D. V0 = V1 + V2 + V3
Question 3
Kirchhoff’s first and second laws are a consequence of the conservation of which quantities?
A. Charge and energy.
B. Charge and resistance.
C. Mass and energy.
D. Mass and resistance.
Question 4
The circuit shown contains three cells of electromotive forces 3.0 V, 2.0 V and 4.0 V, in series with a resistor of resistance 5.0 `Omega`. The cells have negligible internal resistance.
 What is the current I in the circuit?
What is the current I in the circuit?
A. 0.20 A.
B. 0.60 A.
C. 1.0 A.
D. 1.8 A.
Question 5
Four identical resistors are connected in a circuit, as shown. The battery has negligible internal resistance and an e.m.f. of 30 V.
The battery has negligible internal resistance and an e.m.f. of 30 V.
What is the potential difference between the two points X and Y?
Question 6
A battery of negligible internal resistance is connected to three resistors, as shown. The potential difference across each resistor is 2 V.
The potential difference across each resistor is 2 V.
The current from the battery is 0.4 A and the current through one of the resistors connected in parallel is 0.3 A.
What is the current through the other resistor connected in parallel and what is the electromotive force (e.m.f.) of the battery?
| current/A | e.m.f./V | |
|---|---|---|
| A | 0.1 | 4 |
| B | 0.3 | 4 |
| C | 0.1 | 6 |
| D | 0.3 | 6 |
Question 7
Two cells of e.m.f. E1 and E2 and negligible internal resistance are connected into the network as shown. Use Kirchhoff’s laws to state the relation:
Use Kirchhoff’s laws to state the relation:
a. Between currents I1, I2, and I3.
c. Between E1, E2, , I1 and I2 in loop ABCXYZA.
Question 8
The diagram shows a circuit in which the battery has negligible internal resistance. What is the value of the current I ?
What is the value of the current I ?
A. 1.0 A.
B. 1.6 A.
C. 2.0 A.
D. 3.0 A.
Question 9
A cell, two resistors of equal resistance and an ammeter are used to construct four circuits. The resistors are the only parts of the circuits that have resistance. In which circuit will the ammeter show the greatest reading?
Question 10
When four identical resistors are connected as shown in diagram 1, the ammeter reads 1.0 A, and the voltmeter reads zero.  The resistors and meters are reconnected to the supply, as shown in diagram 2.
The resistors and meters are reconnected to the supply, as shown in diagram 2.
What are the meter readings in diagram 2?
| Voltmeter reading/V | Ammeter reading/A | |
|---|---|---|
| A | 0.0 | 1.0 |
| B | 3.0 | 0.5 |
| C | 3.0 | 1.0 |
| D | 6.0 | 0.0 |