Question 1
An astronaut of mass m in a spacecraft experiences a gravitational force F = mg when stationary on the launchpad.
What is the gravitational force on the astronaut when the spacecraft is launched vertically upwards with an acceleration of 0.2g?
A. 1.2mgB. mg
C. 0.8mg
D. 0
Medium
Mark as Complete
Mark Scheme
Question 2
Objects P and Q form an isolated system.
Object P has mass 6.0 kg and is moving at a speed of 3.0 m.s-1.
Object Q has mass 2.0 kg and is moving at a speed of 4.2 m.s-1 at an angle of 35° to the path of P.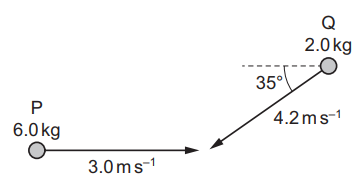 Objects P and Q collide and stick together.
Objects P and Q collide and stick together.
What is the magnitude of the component of the final momentum of the combined objects in the original direction of P?
A. 9.6 kg.m.s–1
B. 11 kg.m.s–1
C. 13 kg.m.s–1
D. 25 kg.m.s–1
Hard
Mark as Complete
Mark Scheme
Question 3
A ball collides with a wall. Before the collision, the ball moves with velocity 8 m.s–1 to the right.
After the collision, it moves with velocity 3 m.s–1 to the left.
What is the change in velocity of the ball during the collision?
A. 5 m.s–1 to the left
B. 5 m.s–1 to the right
C. 11 m.s–1 to the left
D. 11 m.s–1 to the right
Easy
Mark as Complete
Mark Scheme
Question 4
A lead pellet is shot vertically upwards into a clay block that is stationary at the moment of impact, but is able to rise freely after impact.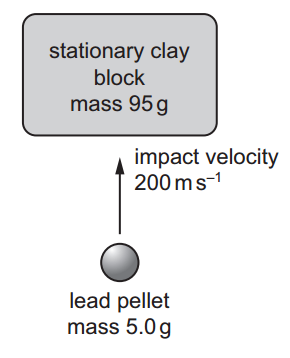 The mass of the pellet is 5.0 g and the mass of the clay block is 95 g.
The mass of the pellet is 5.0 g and the mass of the clay block is 95 g.
The pellet hits the block with an initial vertical velocity of 200 m.s–1. It embeds itself in the block and does not emerge.
How high above its initial position will the block rise?
A. 5.1 m
B. 5.6 m
C. 10 m
D. 100 m
Medium
Mark as Complete
Mark Scheme
Question 5
A ball of mass 2.0 kg travels horizontally with a speed of 4.0 m.s⁻¹. The ball collides with a wall and rebounds in the opposite direction with a speed of 2.8 m.s⁻¹. The time of the collision is 150 ms.
What is the average force exerted on the wall?
A. 16 N
B. 37 N
C. 53 N
D. 91 N
Easy
Mark as Complete
Mark Scheme
Question 6
A moving object strikes a stationary object. The collision is inelastic. The objects move off together.
Assume that the two objects form an isolated system.
Which row shows the possible values of total momentum and total kinetic energy for the system before and after the collision?
| Total momentum before collision/`"kg"."m"."s"^-1` | Total momentum after collision/`"kg"."m"."s"^-1` | Total kinetic energy before collision/J | Total kinetic energy after collision/J | |
|---|---|---|---|---|
| A | 6 | 2 | 90 | 30 |
| B | 6 | 6 | 30 | 90 |
| C | 6 | 6 | 90 | 30 |
| D | 6 | 6 | 90 | 90 |
Medium
Mark as Complete
Mark Scheme
Question 7
Two train carriages each of mass 5000 kg roll toward one another on a horizontal frictionless track. One is travelling at a speed of 2.00 m s⁻¹ and the other at a speed of 1.00 m s⁻¹, as shown.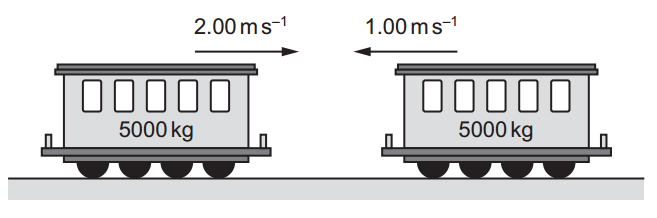 They collide and join together.
They collide and join together.
What is the kinetic energy lost during the collision?
A. 1250 J
B. 7500 J
C. 11 250 J
D. 12 500 J
Medium
Mark as Complete
Mark Scheme
Question 8
A snooker ball of mass 0.20 kg has a collision so that its direction of movement changes by an angle of 90°, as shown.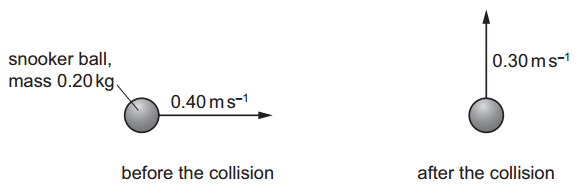 Before the collision, it travels at a speed of 0.40 m.s⁻¹ to the right.
Before the collision, it travels at a speed of 0.40 m.s⁻¹ to the right.
After the collision, it travels at a speed of 0.30 m.s⁻¹ upwards.
What is the magnitude of the change in momentum of the snooker ball?
A. 0.020 kg.m⁻¹
B. 0.10 kg.m⁻¹
C. 0.14 kg.m⁻¹
D. 0.50 kg.m⁻¹
Medium
Mark as Complete
Mark Scheme
Question 9
Which statement is not a requirement of a pair of forces that obey Newton’s third law of motion?
A. The forces act in opposite directions.
B. The forces act on different objects.
C. The forces act on objects in contact.
D. The forces are of equal magnitude.
Medium
Mark as Complete
Mark Scheme
Question 10
A nitrogen molecule P travelling at a speed of 320 m.s–1 in a vacuum collides with a stationary nitrogen molecule Q.
After the collision, P travels at a velocity of 180 m.s–1 at an angle of 55o to its original path.
Q travels in a direction at an angle of 34o to the initial path of P.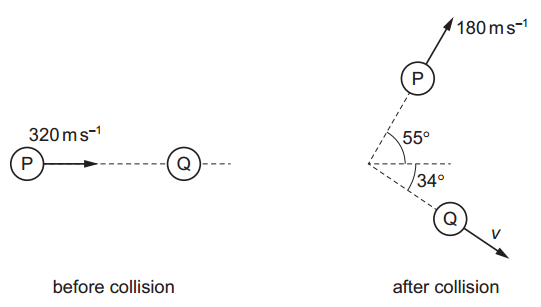 Assume that there are no external forces acting on the molecules.
Assume that there are no external forces acting on the molecules.
What is the magnitude v of the velocity of Q after the collision?
A. 120 m.s–1
B. 140 m.s–1
C. 180 m.s–1
D. 260 m.s–1
Medium
Mark as Complete
Mark Scheme
Question 11
The resultant force acting on an object is slowly increased.
Which graph could show the variation with time t of the momentum p of the object?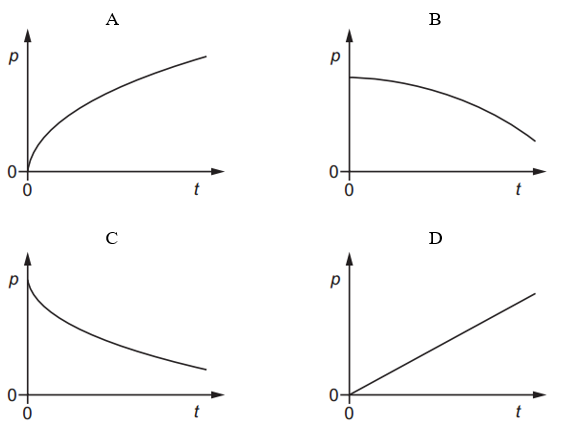
Medium
Mark as Complete
Mark Scheme
Question 12
The table shows four different collisions between two blocks, each of mass 0.50 kg.
Which collision is perfectly elastic?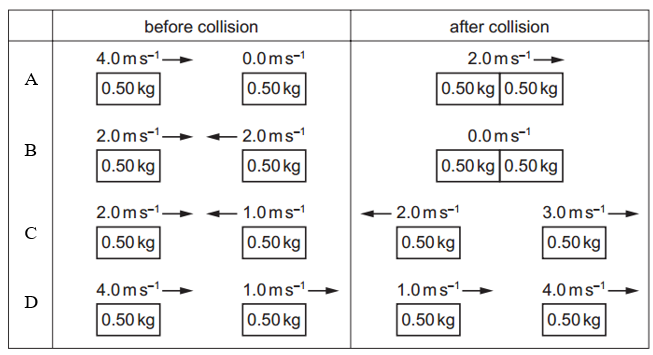
Medium
Mark as Complete
Mark Scheme
Question 13
The diagram shows a ‘ballistic pendulum’. 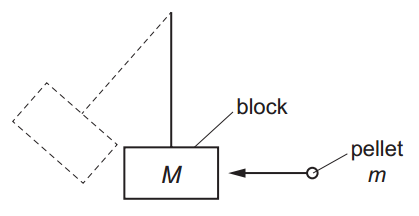 A pellet of mass m travelling at a speed u hits a stationary block of mass M. The pellet becomes embedded in the block and causes the block to move at a speed v immediately after the impact.
A pellet of mass m travelling at a speed u hits a stationary block of mass M. The pellet becomes embedded in the block and causes the block to move at a speed v immediately after the impact.
When a pellet of mass 2m, travelling at a speed 2u, hits a block of mass 2M, what is the speed of the block immediately after the impact? (Neglect the small increase in the mass of the block as the pellet’s mass is added during the collision.)
A. `v`
B. `vsqrt(2)`
C. `2v`
D. `4v`
Medium
Mark as Complete
Mark Scheme
Question 14
A perfectly elastic collision occurs between two objects X and Y. The mass of X is m and the mass of Y is 4m. Object X travels at speed `v` before the collision and speed `(5v)/3` in the opposite direction after the collision. Object Y is stationary before the collision. What is the kinetic energy of Y after the collision?
What is the kinetic energy of Y after the collision?
A. `8/10mv^2`
B. `34/50mv^2`
C. `16/50mv^2`
D. `1/5mv^2`
Medium
Mark as Complete
Mark Scheme
Question 15
An object of mass m travelling with speed 5u collides with, and sticks to, an object of mass 5m travelling in the same direction with speed u.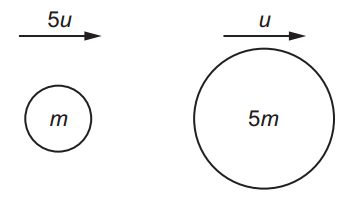 What is the speed with which the two objects travel together in the original direction?
What is the speed with which the two objects travel together in the original direction?
A. `3/10u`
B. `u`
C. `6/5u`
D. `10/6u`
Medium
Mark as Complete
Mark Scheme
Question 16
a. Define momentum.
b. A child stands on a scooter on horizontal ground. The combined mass of the child and the scooter is 16 kg.
The child starts from rest and pushes once on the ground with her foot which causes her to accelerate. The push lasts for a time of 1.1 s. The speed of the child and the scooter after the push is 0.60 m.s–1.
Determine the average resultant force acting horizontally on the child and the scooter during the push.
c. Later, the child in b. travels down a slope at a constant angle to the horizontal, as shown in figure.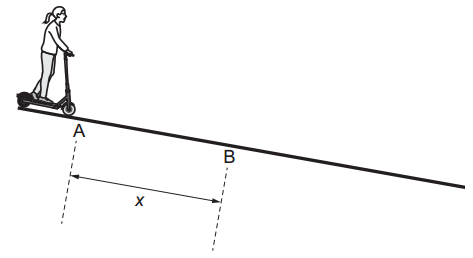 At point A her speed is 0.60m.s–1. She has a constant acceleration of 0.85 m.s–2 parallel to the slope. After a time of 3.7 s, she reaches point B.
At point A her speed is 0.60m.s–1. She has a constant acceleration of 0.85 m.s–2 parallel to the slope. After a time of 3.7 s, she reaches point B.
Calculate the distance `x` travelled by the child along the slope from A to B.
d. At point B, the child in c. applies the brake with a constant force to maintain a constant velocity. Point C is 18 m from point B, as shown in figure.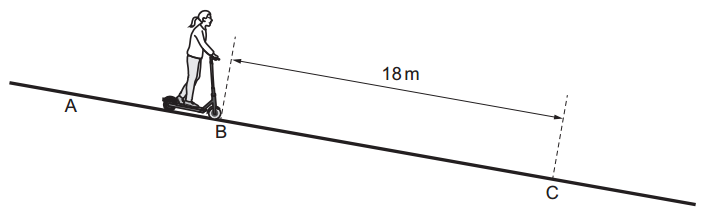 The work done by the braking force between B and C is 250 J.
The work done by the braking force between B and C is 250 J.
i. Determine the magnitude of the braking force.
ii. On figure, sketch the variation of the kinetic energy of the child and scooter with distance travelled from point A to point C.
Numerical values for kinetic energy are not required.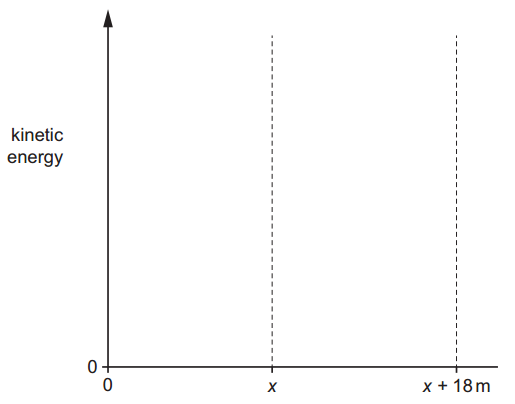
Medium
Mark as Complete
Mark Scheme
Question 17
A ball Y moves along a horizontal frictionless surface and collides with a ball Z, as illustrated in the views from above in figure.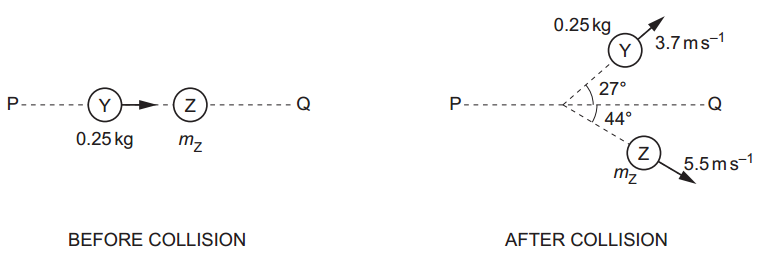
Ball Y has a mass of 0.25 kg and initially moves along a line PQ.
Ball Z has a mass mZ and is initially stationary.
After the collision, ball Y has a final velocity of 3.7 m.s–1 at an angle of 27° to line PQ and ball Z has a final velocity of 5.5 m.s–1 at an angle of 44° to line PQ.
i. Calculate the component of the final momentum of ball Y in the direction perpendicularto line PQ.
ii. By considering the component of the final momentum of each ball in the direction perpendicular to line PQ, calculate mZ.
iii. During the collision, the average force exerted on Y by Z is FY and the average force exerted on Z by Y is FZ.
Compare the magnitudes and directions of FY and FZ. Numerical values are not required.
b. Two blocks, A and B, move directly towards each other along a horizontal frictionless surface, as shown in the view from above in figure. The blocks collide perfectly elastically. Before the collision, block A has a speed of 4 m.s–1 and block B has a speed of 6 m.s–1. After the collision, block B moves back along its original path with a speed of 2 m.s–1.
The blocks collide perfectly elastically. Before the collision, block A has a speed of 4 m.s–1 and block B has a speed of 6 m.s–1. After the collision, block B moves back along its original path with a speed of 2 m.s–1.
Calculate the speed of block A after the collision.
Medium
Mark as Complete
Mark Scheme
Question 18
A horizontal spring is fixed at one end. A block is pushed against the other end of the spring so that the spring is compressed, as shown in figure. The block is released and accelerates along a horizontal frictionless surface as the spring returns to its original length. The block leaves the end of the spring with a speed of 2.3 m.s–1, as shown in figure.
The block is released and accelerates along a horizontal frictionless surface as the spring returns to its original length. The block leaves the end of the spring with a speed of 2.3 m.s–1, as shown in figure.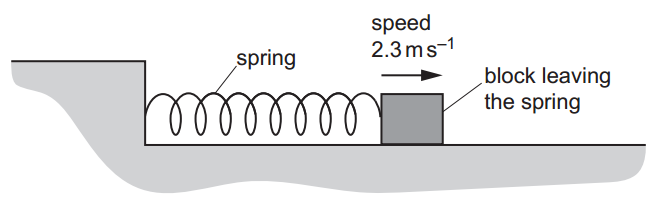 The block has a mass of 250 g and the spring has a spring constant of 420 N.m–1. Assume that the spring always obeys Hooke’s law and that all the elastic potential energy of the spring is transferred to the kinetic energy of the block.
The block has a mass of 250 g and the spring has a spring constant of 420 N.m–1. Assume that the spring always obeys Hooke’s law and that all the elastic potential energy of the spring is transferred to the kinetic energy of the block.
a. Calculate the kinetic energy of the block as it leaves the spring.
b. Calculate the compression of the spring immediately before the block is released.
c. After leaving the spring, the block moves along the surface until it hits a barrier at a speed of 2.3 m.s–1. The block then rebounds at a speed of 1.5 m.s–1 and moves back along its original path. The block is in contact with the barrier for a time of 0.086 s.
Calculate:
i. The change in momentum of the block during the collision.
ii. The average resultant force exerted on the block during the collision.
d. The maximum compression x of the spring is now varied in order to vary the kinetic energy EK of the block as it leaves the spring. Assume that all the elastic potential energy in the spring is always transferred to the kinetic energy of the block.
On figure, sketch a graph to show the variation with x of EK
Medium
Mark as Complete
Mark Scheme
Question 19
A block is pulled by a force X in a straight line along a rough horizontal surface, as shown in figure.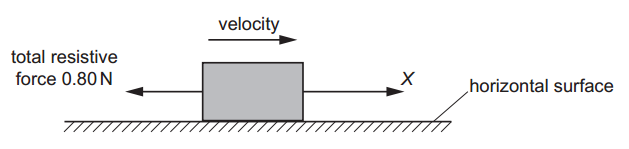 Assume that the total resistive force opposing the motion of the block is 0.80 N at all speeds of the block.
Assume that the total resistive force opposing the motion of the block is 0.80 N at all speeds of the block.
The variation with time t of the magnitude of the force X is shown in figure.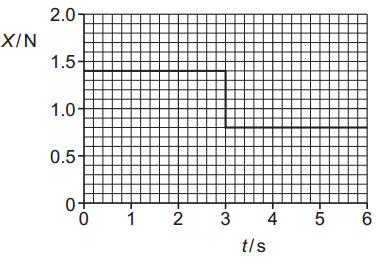 a. i. Define force.
a. i. Define force.
ii. Determine the change in momentum of the block from time t = 0 to time t = 3.0 s.
b. i. Describe and explain the motion of the block between time t = 3.0 s and time t = 6.0 s.
ii. Force X produces a total power of 2.0 W when moving the block between time t = 3.0 s and time t = 6.0 s.
Calculate the distance moved by the block during this time interval.
c. The block is at rest at time t = 0.
On figure, sketch a graph to show the variation of the momentum of the block with time t from t = 0 to t = 6.0 s.
Numerical values of momentum are not required.
Medium
Mark as Complete
Mark Scheme
Question 20
a. State Newton’s first law.
b. A log of mass 450 kg is pulled up a slope by a wire attached to a motor, as shown in figure.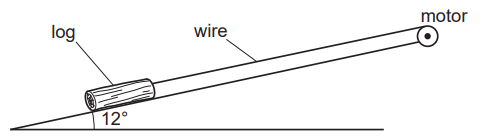 The angle that the slope makes with the horizontal is 12°. The frictional force acting on the log is 650 N. The log travels with constant velocity.
The angle that the slope makes with the horizontal is 12°. The frictional force acting on the log is 650 N. The log travels with constant velocity.
i. With reference to the motion of the log, discuss whether the log is in equilibrium.
ii. Calculate the tension in the wire.
Medium
Mark as Complete
Mark Scheme
Question 1
An astronaut of mass m in a spacecraft experiences a gravitational force F = mg when stationary on the launchpad.
What is the gravitational force on the astronaut when the spacecraft is launched vertically upwards with an acceleration of 0.2g?
A. 1.2mgB. mg
C. 0.8mg
D. 0
Answer: A
The gravitational force acting on the astronaut never changes just because the spacecraft is accelerating.
It is still:`F_("gravity") = m g`
However, the apparent weight (the normal contact force the astronaut feels) increases due to the upward acceleration.
When the spacecraft accelerates upward with acceleration a = 0.2g
The total net upward force needed is: `F_("net") = m a = m (0.2 g)`
The reaction force (i.e. what the astronaut feels pressing back): `F_("reaction") = m g + m (0.2 g) = 1.2 m g`
Question 2
Objects P and Q form an isolated system.
Object P has mass 6.0 kg and is moving at a speed of 3.0 m.s-1.
Object Q has mass 2.0 kg and is moving at a speed of 4.2 m.s-1 at an angle of 35° to the path of P. Objects P and Q collide and stick together.
Objects P and Q collide and stick together.
What is the magnitude of the component of the final momentum of the combined objects in the original direction of P?
A. 9.6 kg.m.s–1
B. 11 kg.m.s–1
C. 13 kg.m.s–1
D. 25 kg.m.s–1
Answer: C
We'll split the motion of Q into:
Horizontal component: uQ,x = 4.2cos(35∘)Vertical component: uQ,y = 4.2sin(35∘)
Initial total momentum in the x-direction:
`p_("x,initial") = m_P u_P + m_Q u_Q cos(35^@)=6 xx3 + 2 xx 4.2 xx cos(35^@)`
`= 18 + 6.88 = 24.88 " kg.m.s"^-1`
Resolve vertical momenta:
`0 = 2 xx 4.2 xx sin(35^@) - 8 xx v_("y")`
`v_("y") = (2 xx 4.2 xx sin(35^@)) / 8 = 0.60 " m.s"^-1`
Let `v` be the speed of the combined object after collision, and θ is the angle to the x-axis. We find horizontal component:
`p_("x,final") = (m_P + m_Q) xx vcos(theta)`
Total final mass: kg
Resultant speed: `v = sqrt(0.6^2 + (24.88 / 8)^2) = sqrt(10.04)=3.17 " m"."s"^-1`
`p_("x,final") = 8 xx 3.17cos(theta) = 13 " kg.m.s"^-1`
Question 3
A ball collides with a wall. Before the collision, the ball moves with velocity 8 m.s–1 to the right.
After the collision, it moves with velocity 3 m.s–1 to the left.
What is the change in velocity of the ball during the collision?
A. 5 m.s–1 to the left
B. 5 m.s–1 to the right
C. 11 m.s–1 to the left
D. 11 m.s–1 to the right
Answer: C
We define the direction to the right as positive, and to the left as negative.
Change in velocity: `Delta v = v - u = -3 - 8 = -11 " m.s"^-1`
Question 4
A lead pellet is shot vertically upwards into a clay block that is stationary at the moment of impact, but is able to rise freely after impact. The mass of the pellet is 5.0 g and the mass of the clay block is 95 g.
The mass of the pellet is 5.0 g and the mass of the clay block is 95 g.
The pellet hits the block with an initial vertical velocity of 200 m.s–1. It embeds itself in the block and does not emerge.
How high above its initial position will the block rise?
A. 5.1 m
B. 5.6 m
C. 10 m
D. 100 m
Answer: A
Conservation of momentum at the point of impact:
`m_1 u_1 + m_2 u_2 = (m_1 + m_2)v`
`0.005 xx 200 = 0.1 xx v => v = 10 " m"."s"^-1`
Apply conservation of energy to find how high it rises:
`1/2m v^2 = mg h => h = v^2 / (2g)`
`h = 10^2 / (2 xx 9.8) = 100 / 19.6 = "5.1 m"`
Question 5
A ball of mass 2.0 kg travels horizontally with a speed of 4.0 m.s⁻¹. The ball collides with a wall and rebounds in the opposite direction with a speed of 2.8 m.s⁻¹. The time of the collision is 150 ms.
What is the average force exerted on the wall?
A. 16 N
B. 37 N
C. 53 N
D. 91 N
Answer: D
Change in momentum: `Δp = m(v - u) = 2.0 xx (-2.8 - 4.0) = 2.0 xx (-6.8) = -13.6 " kg.m.s"^-1`
`F = |Δp| / (Δt) = 13.6 / 0.150 = "91 N"`
Question 6
A moving object strikes a stationary object. The collision is inelastic. The objects move off together.
Assume that the two objects form an isolated system.
Which row shows the possible values of total momentum and total kinetic energy for the system before and after the collision?
| Total momentum before collision/`"kg"."m"."s"^-1` | Total momentum after collision/`"kg"."m"."s"^-1` | Total kinetic energy before collision/J | Total kinetic energy after collision/J | |
|---|---|---|---|---|
| A | 6 | 2 | 90 | 30 |
| B | 6 | 6 | 30 | 90 |
| C | 6 | 6 | 90 | 30 |
| D | 6 | 6 | 90 | 90 |
Answer: C
Momentum is conserved in all collisions if the system is isolated:
Initial momentum = Final momentum (6 = 6).
Kinetic energy is not conserved in inelastic collisions (because some of it is converted into other forms like heat, sound, deformation).
`K_("initial") = 90`, `K_("final") = 30`
Question 7
Two train carriages each of mass 5000 kg roll toward one another on a horizontal frictionless track. One is travelling at a speed of 2.00 m s⁻¹ and the other at a speed of 1.00 m s⁻¹, as shown. They collide and join together.
They collide and join together.
What is the kinetic energy lost during the collision?
A. 1250 J
B. 7500 J
C. 11 250 J
D. 12 500 J
Answer: C
Take rightward direction as positive.
Initial momentum: `p = m_1 u_1 + m_2 u_2 = 5000 xx 2 - 5000 xx 1 = 5000 " kg"."m"."s"^-1`
Total mass after collision: `m = 5000 + 5000 = "10000 kg"`
Final velocity after inelastic collision: `v = 5000 / 10000 = 0.5 " m"."s"^-1`
Kinetic energy before collision:
`KE_1 = 1/2 xx 5000 xx (2)^2 = "10000 J"`
`KE_2 = 1/2 xx 5000 xx (1)^2 = "2500 J"`
Total initial KE: `KE_("initial") = 10000 + 2500 = "12500 J"`
Kinetic energy after collision: `KE_("final") = 1/2 xx 10000 xx (0.5)^2 = "1250 J"`
Kinetic energy lost: `\Delta KE = 12500 - 1250 = "11250 J"`
Question 8
A snooker ball of mass 0.20 kg has a collision so that its direction of movement changes by an angle of 90°, as shown. Before the collision, it travels at a speed of 0.40 m.s⁻¹ to the right.
Before the collision, it travels at a speed of 0.40 m.s⁻¹ to the right.
After the collision, it travels at a speed of 0.30 m.s⁻¹ upwards.
What is the magnitude of the change in momentum of the snooker ball?
A. 0.020 kg.m⁻¹
B. 0.10 kg.m⁻¹
C. 0.14 kg.m⁻¹
D. 0.50 kg.m⁻¹
Answer: B
Initial momentum: `p_1 = 0.20 xx 0.40 = 0.080 " kg"."m"^-1`
Final momentum: `p_2 = 0.20 xx 0.30 = 0.060 " kg"."m"^-1`
Change in momentum (vector):
Since the vectors are perpendicular:
`\Delta p = sqrt((0.080)^2 + (0.060)^2) = sqrt(0.0100) = 0.10 " kg"."m"^-1`
Question 9
Which statement is not a requirement of a pair of forces that obey Newton’s third law of motion?
A. The forces act in opposite directions.
B. The forces act on different objects.
C. The forces act on objects in contact.
D. The forces are of equal magnitude.
Answer: C
A. Incorrect
Newton's third law requires that the forces act in opposite directions.
Example: You push on a wall, the wall pushes back on you.
`F_("A on B") = -F_("B on A")`
B. Incorrect
Newton’s third law forces always act on two different objects, never on the same one.
The action is on one object; the reaction is on the other.
C. Correct
This is the correct answer because contact is not required.
Newton’s third law also applies to non-contact forces, like gravity, electrostatic forces, or magnetic forces.
For example: Earth pulls on the Moon, and the Moon pulls back on the Earth — no contact needed.
D. Incorrect
Newton’s third law states the forces are equal in magnitude.
Question 10
A nitrogen molecule P travelling at a speed of 320 m.s–1 in a vacuum collides with a stationary nitrogen molecule Q.
After the collision, P travels at a velocity of 180 m.s–1 at an angle of 55o to its original path.
Q travels in a direction at an angle of 34o to the initial path of P. Assume that there are no external forces acting on the molecules.
Assume that there are no external forces acting on the molecules.
What is the magnitude v of the velocity of Q after the collision?
A. 120 m.s–1
B. 140 m.s–1
C. 180 m.s–1
D. 260 m.s–1
Answer: D
Momentum in x-direction (horizontal):
Before collision:
P: `p_x = 320m`
Q: `p_x = 0`
After collision:
P: `180m xx cos(55°)`
Q: `v xx cos(34°)`
Using conservation: `320 = 180 xxcos(55°) + v xx cos(34°)`
`v = 216.7 / 0.829 ≈ 261.4" m"."s"^-1`
Momentum in y-direction (vertical):
Before collision: No vertical momentum.
After collision:
P: `180 xx sin(55°)` upward.
Q: `v xx sin(34°)` downward.
Using conservation: `180 xx sin(55^@) = v xxsin(34^@)`
`v = 147.5 / 0.559 ≈ 263.8 " m"."s"^-1`
Question 11
The resultant force acting on an object is slowly increased.
Which graph could show the variation with time t of the momentum p of the object?
Answer: B
A. Incorrect: This shows momentum increasing quickly at first, then slowing down - which implies decreasing force.
B. Correct: Rate of change of momentum is directly proportional to the force.
If the force is slowly increasing, then the gradient of the p–t graph is also increasing slowly.
That means:
Momentum increases more slowly at first.
Then it increases faster as time goes on.
This shape is a gradually steepening curve, concave down, matching Graph B.
C. Incorrect: Momentum is decreasing over time, which would require a net force in the opposite direction, not an increasing one.
D. Incorrect:
A straight line means a constant force. But the question says force is increasing, so the line should curve upward.
Question 12
The table shows four different collisions between two blocks, each of mass 0.50 kg.
Which collision is perfectly elastic?
Answer: D
A perfectly elastic collision must satisfy two conditions:
Conservation of momentum.
Conservation of kinetic energy.
Eliminate A and B because those are inelastic collision.
Check option D:
Before collision:
Block 1:
`KE_1 = 1/2 xx 0.5 xx 4.0^2 = "4.0 J"`
Block 2:
`KE_2 = 1/2 xx 0.5 xx 1.0^2 = "0.25 J"`
Total KE before = 4.0 + 0.25 = 4.25 J
After collision:
Block 1:
`KE_1 = 1/2 xx 0.5 xx 1.0^2 = "0.25 J"`
Block 2:
`KE_2 = 1/2 xx 0.5 xx 4.0^2 = "4.0 J"`
Total KE after = 0.25 + 4.0 = 4.25 J
Kinetic energy is conserved.
Momentum before the collision: `p = (0.5 × 4.0) + (0.5 × 1.0) = 2.0 + 0.5 = 2.5 " kg"."m"."s"^-1`
Momentum after the collision: `p = (0.5 × 1.0) + (0.5 × 4.0) = 0.5 + 2.0 = 2.5 "kg"."m"."s"^-1`
Momentum is conserved.
Question 13
The diagram shows a ‘ballistic pendulum’.  A pellet of mass m travelling at a speed u hits a stationary block of mass M. The pellet becomes embedded in the block and causes the block to move at a speed v immediately after the impact.
A pellet of mass m travelling at a speed u hits a stationary block of mass M. The pellet becomes embedded in the block and causes the block to move at a speed v immediately after the impact.
When a pellet of mass 2m, travelling at a speed 2u, hits a block of mass 2M, what is the speed of the block immediately after the impact? (Neglect the small increase in the mass of the block as the pellet’s mass is added during the collision.)
A. `v`
B. `vsqrt(2)`
C. `2v`
D. `4v`
Answer: C
Before collision:
Pellet mass = 2m, velocity = 2u
Block mass = 2M, velocity = 0
After collision:
Combined mass = 2m + 2M, velocity = v'
Apply conservation of momentum: `2m xx 2u = (2m + 2M) xx v'`
`v' = (4m u)/(2m + 2M)`
Factor denominator:
`v' = (4m u)/(2(m + M)) = (2m u)/(m + M)= (4m u)/(2(m + M)) = (2m u)/(m + M)=2v`
Question 14
A perfectly elastic collision occurs between two objects X and Y. The mass of X is m and the mass of Y is 4m. Object X travels at speed `v` before the collision and speed `(5v)/3` in the opposite direction after the collision. Object Y is stationary before the collision. What is the kinetic energy of Y after the collision?
What is the kinetic energy of Y after the collision?
A. `8/10mv^2`
B. `34/50mv^2`
C. `16/50mv^2`
D. `1/5mv^2`
Answer: C
Before collision: `p_("initial") = m v`
After collision: `p_("final") = m((-3v)/5) + 4mv_y`
Conservation of momentum: `m v = -3mv/5 + 4m v_y`
`v = -v3/5 + 4v_y`
`v_y = (2v)/5`
Kinetic energy of Y after collision:
`KE_Y = (1/2) xx 4m xx ((2v)/5)^2 = 2m xx (4v^2)/25 = (8mv^2)/25=16/50mv^2`
Question 15
An object of mass m travelling with speed 5u collides with, and sticks to, an object of mass 5m travelling in the same direction with speed u. What is the speed with which the two objects travel together in the original direction?
What is the speed with which the two objects travel together in the original direction?
A. `3/10u`
B. `u`
C. `6/5u`
D. `10/6u`
Answer: D
Total momentum before collision: `p_("total") = 5m u + 5m u = 10 m u`
Total momentum after collision: `p_("after") = 6m v`
Momentum conservation: `6m v = 10m u`
`v = 10/6 u`
Question 16
a. Define momentum.
b. A child stands on a scooter on horizontal ground. The combined mass of the child and the scooter is 16 kg.
The child starts from rest and pushes once on the ground with her foot which causes her to accelerate. The push lasts for a time of 1.1 s. The speed of the child and the scooter after the push is 0.60 m.s–1.
Determine the average resultant force acting horizontally on the child and the scooter during the push.
c. Later, the child in b. travels down a slope at a constant angle to the horizontal, as shown in figure. At point A her speed is 0.60m.s–1. She has a constant acceleration of 0.85 m.s–2 parallel to the slope. After a time of 3.7 s, she reaches point B.
At point A her speed is 0.60m.s–1. She has a constant acceleration of 0.85 m.s–2 parallel to the slope. After a time of 3.7 s, she reaches point B.
Calculate the distance `x` travelled by the child along the slope from A to B.
d. At point B, the child in c. applies the brake with a constant force to maintain a constant velocity. Point C is 18 m from point B, as shown in figure. The work done by the braking force between B and C is 250 J.
The work done by the braking force between B and C is 250 J.
i. Determine the magnitude of the braking force.
ii. On figure, sketch the variation of the kinetic energy of the child and scooter with distance travelled from point A to point C.
Numerical values for kinetic energy are not required.
a. Momentum is defined as the product of mass and velocity of an object.
b. `F = (m xx Δv) / (Δt)=(16 xx 0.60) / 1.1 = "8.7 N"`
c. `x = u t + (1/2) a t^2 =0.60 xx3.7 + 0.5 xx 0.85 xx 3.7^2 ="8 m"`
d. i. `F = W / d = 250 / 18 = "14 N"`
ii. 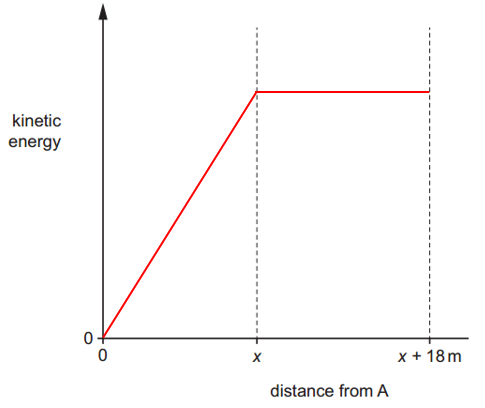
Question 17
A ball Y moves along a horizontal frictionless surface and collides with a ball Z, as illustrated in the views from above in figure.
Ball Y has a mass of 0.25 kg and initially moves along a line PQ.
Ball Z has a mass mZ and is initially stationary.
After the collision, ball Y has a final velocity of 3.7 m.s–1 at an angle of 27° to line PQ and ball Z has a final velocity of 5.5 m.s–1 at an angle of 44° to line PQ.
i. Calculate the component of the final momentum of ball Y in the direction perpendicularto line PQ.
ii. By considering the component of the final momentum of each ball in the direction perpendicular to line PQ, calculate mZ.
iii. During the collision, the average force exerted on Y by Z is FY and the average force exerted on Z by Y is FZ.
Compare the magnitudes and directions of FY and FZ. Numerical values are not required.
b. Two blocks, A and B, move directly towards each other along a horizontal frictionless surface, as shown in the view from above in figure. The blocks collide perfectly elastically. Before the collision, block A has a speed of 4 m.s–1 and block B has a speed of 6 m.s–1. After the collision, block B moves back along its original path with a speed of 2 m.s–1.
The blocks collide perfectly elastically. Before the collision, block A has a speed of 4 m.s–1 and block B has a speed of 6 m.s–1. After the collision, block B moves back along its original path with a speed of 2 m.s–1.
Calculate the speed of block A after the collision.
a. i. `p = 0.25 xx 3.7 xx sin(27) = 0.42 " kg"."m"."s"^-1`
ii. Conservation of momentum in direction perpendicular to PQ:
momentum of Y = momentum of Z
`0.25 xx 3.7 xx sin(27) = m_Z xx5.5 xx sin(44)`
`m_Z = 0.42 / (5.5 xx 0.694) = "0.11 kg"`
iii. According to Newton’s Third Law, the forces are equal in magnitude and act in opposite directions.
Magnitudes: equal.
Directions: opposite.
b. Before collision:
A moves at 4 m.s-1 to the right
B moves at 6 m.s-1 to the left
After collision:
B moves at 2 m.s-1 to the left
A = unknown speed `v`
Since it’s a perfectly elastic collision, use conservation of momentum (take right as positive):
`4m - 6m = m v - 2m`
`-2m = m v - 2m`
`v = 8 " m"."s"^-1`
Question 18
A horizontal spring is fixed at one end. A block is pushed against the other end of the spring so that the spring is compressed, as shown in figure. The block is released and accelerates along a horizontal frictionless surface as the spring returns to its original length. The block leaves the end of the spring with a speed of 2.3 m.s–1, as shown in figure.
The block is released and accelerates along a horizontal frictionless surface as the spring returns to its original length. The block leaves the end of the spring with a speed of 2.3 m.s–1, as shown in figure. The block has a mass of 250 g and the spring has a spring constant of 420 N.m–1. Assume that the spring always obeys Hooke’s law and that all the elastic potential energy of the spring is transferred to the kinetic energy of the block.
The block has a mass of 250 g and the spring has a spring constant of 420 N.m–1. Assume that the spring always obeys Hooke’s law and that all the elastic potential energy of the spring is transferred to the kinetic energy of the block.
a. Calculate the kinetic energy of the block as it leaves the spring.
b. Calculate the compression of the spring immediately before the block is released.
c. After leaving the spring, the block moves along the surface until it hits a barrier at a speed of 2.3 m.s–1. The block then rebounds at a speed of 1.5 m.s–1 and moves back along its original path. The block is in contact with the barrier for a time of 0.086 s.
Calculate:
i. The change in momentum of the block during the collision.
ii. The average resultant force exerted on the block during the collision.
d. The maximum compression x of the spring is now varied in order to vary the kinetic energy EK of the block as it leaves the spring. Assume that all the elastic potential energy in the spring is always transferred to the kinetic energy of the block.
On figure, sketch a graph to show the variation with x of EK
a. `E_k = 1/2 xx 0.25 xx 2.3^2 = "0.66 J"`
b. We assume elastic potential energy = kinetic energy:
`E = 1/2xx kxx x^2`
`x^2 = 0.66 / (0.5 xx 420) = 0.00314`
`rightarrowx = sqrt(0.00314) = "0.056 m"`
c. i. Let initial velocity be +2.3 m.s-1 (forward), final = `-1.5` m.s-1 (backward)
`Δp = m(v_f - v_i) = 0.25 xx(-1.5 - 2.3) = -"0.95 N.s"`
`|Δp| = " 0.95 N.s"`
ii. `F = (Δp) / (Δt )= 0.95 / 0.086 = "11 N"`
d. 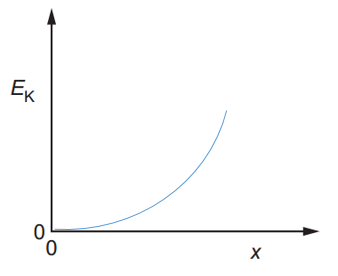
Question 19
A block is pulled by a force X in a straight line along a rough horizontal surface, as shown in figure. Assume that the total resistive force opposing the motion of the block is 0.80 N at all speeds of the block.
Assume that the total resistive force opposing the motion of the block is 0.80 N at all speeds of the block.
The variation with time t of the magnitude of the force X is shown in figure. a. i. Define force.
a. i. Define force.
ii. Determine the change in momentum of the block from time t = 0 to time t = 3.0 s.
b. i. Describe and explain the motion of the block between time t = 3.0 s and time t = 6.0 s.
ii. Force X produces a total power of 2.0 W when moving the block between time t = 3.0 s and time t = 6.0 s.
Calculate the distance moved by the block during this time interval.
c. The block is at rest at time t = 0.
On figure, sketch a graph to show the variation of the momentum of the block with time t from t = 0 to t = 6.0 s.
Numerical values of momentum are not required.
a. i. Force is the rate of change of momentum of an object.
ii. `F_("net") =F_X-F_("resistive")= 1.4 - 0.80 = "0.60 N"`
Change in momentum: `Delta p = 0.60 xx 3.0 = 1.8 " kg.m.s"^-1`
b. i. At t = 3.0 s, the applied force equals the resistive force. This gives zero net force.
Therefore, no acceleration. The block moves at constant speed.
ii. `v = P / F = 2.0 / 0.80 = 2.5 " m.s"^-1`
`x = v xx t = 2.5 xx 3.0 = "7.5 m"`
c. 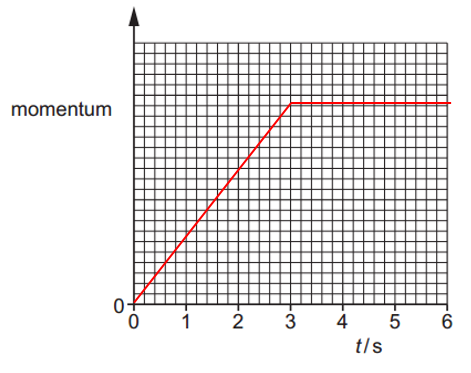
Question 20
a. State Newton’s first law.
b. A log of mass 450 kg is pulled up a slope by a wire attached to a motor, as shown in figure. The angle that the slope makes with the horizontal is 12°. The frictional force acting on the log is 650 N. The log travels with constant velocity.
The angle that the slope makes with the horizontal is 12°. The frictional force acting on the log is 650 N. The log travels with constant velocity.
i. With reference to the motion of the log, discuss whether the log is in equilibrium.
ii. Calculate the tension in the wire.
a. A body continues in a state of rest or uniform motion in a straight line unless acted on by a resultant (external) force.
b. i. Equilibrium condition:
The log moves with constant velocity.
This means acceleration = 0.
Therefore, the resultant force acting on the log is zero.
Since there is no net force and no angular acceleration, the log is in equilibrium.
ii. We resolve forces along the slope.
Weight component down the slope:
`W_("parallel") =mgsintheta=450 xx 9.81 xx sin(12°) = "917.8 N"`
Frictional force = 650 N
Since the log is in equilibrium, the tension in the wire must balance the sum of friction and weight component:
`T =W_("parallel")+F_("friction")= 917.8 + 650 = "1570 N"`
Question 1
An astronaut of mass m in a spacecraft experiences a gravitational force F = mg when stationary on the launchpad.
What is the gravitational force on the astronaut when the spacecraft is launched vertically upwards with an acceleration of 0.2g?
A. 1.2mgB. mg
C. 0.8mg
D. 0
Question 2
Objects P and Q form an isolated system.
Object P has mass 6.0 kg and is moving at a speed of 3.0 m.s-1.
Object Q has mass 2.0 kg and is moving at a speed of 4.2 m.s-1 at an angle of 35° to the path of P. Objects P and Q collide and stick together.
Objects P and Q collide and stick together.
What is the magnitude of the component of the final momentum of the combined objects in the original direction of P?
A. 9.6 kg.m.s–1
B. 11 kg.m.s–1
C. 13 kg.m.s–1
D. 25 kg.m.s–1
Question 3
A ball collides with a wall. Before the collision, the ball moves with velocity 8 m.s–1 to the right.
After the collision, it moves with velocity 3 m.s–1 to the left.
What is the change in velocity of the ball during the collision?
A. 5 m.s–1 to the left
B. 5 m.s–1 to the right
C. 11 m.s–1 to the left
D. 11 m.s–1 to the right
Question 4
A lead pellet is shot vertically upwards into a clay block that is stationary at the moment of impact, but is able to rise freely after impact. The mass of the pellet is 5.0 g and the mass of the clay block is 95 g.
The mass of the pellet is 5.0 g and the mass of the clay block is 95 g.
The pellet hits the block with an initial vertical velocity of 200 m.s–1. It embeds itself in the block and does not emerge.
How high above its initial position will the block rise?
A. 5.1 m
B. 5.6 m
C. 10 m
D. 100 m
Question 5
A ball of mass 2.0 kg travels horizontally with a speed of 4.0 m.s⁻¹. The ball collides with a wall and rebounds in the opposite direction with a speed of 2.8 m.s⁻¹. The time of the collision is 150 ms.
What is the average force exerted on the wall?
A. 16 N
B. 37 N
C. 53 N
D. 91 N
Question 6
A moving object strikes a stationary object. The collision is inelastic. The objects move off together.
Assume that the two objects form an isolated system.
Which row shows the possible values of total momentum and total kinetic energy for the system before and after the collision?
| Total momentum before collision/`"kg"."m"."s"^-1` | Total momentum after collision/`"kg"."m"."s"^-1` | Total kinetic energy before collision/J | Total kinetic energy after collision/J | |
|---|---|---|---|---|
| A | 6 | 2 | 90 | 30 |
| B | 6 | 6 | 30 | 90 |
| C | 6 | 6 | 90 | 30 |
| D | 6 | 6 | 90 | 90 |
Question 7
Two train carriages each of mass 5000 kg roll toward one another on a horizontal frictionless track. One is travelling at a speed of 2.00 m s⁻¹ and the other at a speed of 1.00 m s⁻¹, as shown. They collide and join together.
They collide and join together.
What is the kinetic energy lost during the collision?
A. 1250 J
B. 7500 J
C. 11 250 J
D. 12 500 J
Question 8
A snooker ball of mass 0.20 kg has a collision so that its direction of movement changes by an angle of 90°, as shown. Before the collision, it travels at a speed of 0.40 m.s⁻¹ to the right.
Before the collision, it travels at a speed of 0.40 m.s⁻¹ to the right.
After the collision, it travels at a speed of 0.30 m.s⁻¹ upwards.
What is the magnitude of the change in momentum of the snooker ball?
A. 0.020 kg.m⁻¹
B. 0.10 kg.m⁻¹
C. 0.14 kg.m⁻¹
D. 0.50 kg.m⁻¹
Question 9
Which statement is not a requirement of a pair of forces that obey Newton’s third law of motion?
A. The forces act in opposite directions.
B. The forces act on different objects.
C. The forces act on objects in contact.
D. The forces are of equal magnitude.
Question 10
A nitrogen molecule P travelling at a speed of 320 m.s–1 in a vacuum collides with a stationary nitrogen molecule Q.
After the collision, P travels at a velocity of 180 m.s–1 at an angle of 55o to its original path.
Q travels in a direction at an angle of 34o to the initial path of P. Assume that there are no external forces acting on the molecules.
Assume that there are no external forces acting on the molecules.
What is the magnitude v of the velocity of Q after the collision?
A. 120 m.s–1
B. 140 m.s–1
C. 180 m.s–1
D. 260 m.s–1
Question 11
The resultant force acting on an object is slowly increased.
Which graph could show the variation with time t of the momentum p of the object?
Question 12
The table shows four different collisions between two blocks, each of mass 0.50 kg.
Which collision is perfectly elastic?
Question 13
The diagram shows a ‘ballistic pendulum’.  A pellet of mass m travelling at a speed u hits a stationary block of mass M. The pellet becomes embedded in the block and causes the block to move at a speed v immediately after the impact.
A pellet of mass m travelling at a speed u hits a stationary block of mass M. The pellet becomes embedded in the block and causes the block to move at a speed v immediately after the impact.
When a pellet of mass 2m, travelling at a speed 2u, hits a block of mass 2M, what is the speed of the block immediately after the impact? (Neglect the small increase in the mass of the block as the pellet’s mass is added during the collision.)
A. `v`
B. `vsqrt(2)`
C. `2v`
D. `4v`
Question 14
A perfectly elastic collision occurs between two objects X and Y. The mass of X is m and the mass of Y is 4m. Object X travels at speed `v` before the collision and speed `(5v)/3` in the opposite direction after the collision. Object Y is stationary before the collision. What is the kinetic energy of Y after the collision?
What is the kinetic energy of Y after the collision?
A. `8/10mv^2`
B. `34/50mv^2`
C. `16/50mv^2`
D. `1/5mv^2`
Question 15
An object of mass m travelling with speed 5u collides with, and sticks to, an object of mass 5m travelling in the same direction with speed u. What is the speed with which the two objects travel together in the original direction?
What is the speed with which the two objects travel together in the original direction?
A. `3/10u`
B. `u`
C. `6/5u`
D. `10/6u`
Question 16
a. Define momentum.
b. A child stands on a scooter on horizontal ground. The combined mass of the child and the scooter is 16 kg.
The child starts from rest and pushes once on the ground with her foot which causes her to accelerate. The push lasts for a time of 1.1 s. The speed of the child and the scooter after the push is 0.60 m.s–1.
Determine the average resultant force acting horizontally on the child and the scooter during the push.
c. Later, the child in b. travels down a slope at a constant angle to the horizontal, as shown in figure. At point A her speed is 0.60m.s–1. She has a constant acceleration of 0.85 m.s–2 parallel to the slope. After a time of 3.7 s, she reaches point B.
At point A her speed is 0.60m.s–1. She has a constant acceleration of 0.85 m.s–2 parallel to the slope. After a time of 3.7 s, she reaches point B.
Calculate the distance `x` travelled by the child along the slope from A to B.
d. At point B, the child in c. applies the brake with a constant force to maintain a constant velocity. Point C is 18 m from point B, as shown in figure. The work done by the braking force between B and C is 250 J.
The work done by the braking force between B and C is 250 J.
i. Determine the magnitude of the braking force.
ii. On figure, sketch the variation of the kinetic energy of the child and scooter with distance travelled from point A to point C.
Numerical values for kinetic energy are not required.
Question 17
A ball Y moves along a horizontal frictionless surface and collides with a ball Z, as illustrated in the views from above in figure.
Ball Y has a mass of 0.25 kg and initially moves along a line PQ.
Ball Z has a mass mZ and is initially stationary.
After the collision, ball Y has a final velocity of 3.7 m.s–1 at an angle of 27° to line PQ and ball Z has a final velocity of 5.5 m.s–1 at an angle of 44° to line PQ.
i. Calculate the component of the final momentum of ball Y in the direction perpendicularto line PQ.
ii. By considering the component of the final momentum of each ball in the direction perpendicular to line PQ, calculate mZ.
iii. During the collision, the average force exerted on Y by Z is FY and the average force exerted on Z by Y is FZ.
Compare the magnitudes and directions of FY and FZ. Numerical values are not required.
b. Two blocks, A and B, move directly towards each other along a horizontal frictionless surface, as shown in the view from above in figure. The blocks collide perfectly elastically. Before the collision, block A has a speed of 4 m.s–1 and block B has a speed of 6 m.s–1. After the collision, block B moves back along its original path with a speed of 2 m.s–1.
The blocks collide perfectly elastically. Before the collision, block A has a speed of 4 m.s–1 and block B has a speed of 6 m.s–1. After the collision, block B moves back along its original path with a speed of 2 m.s–1.
Calculate the speed of block A after the collision.
Question 18
A horizontal spring is fixed at one end. A block is pushed against the other end of the spring so that the spring is compressed, as shown in figure. The block is released and accelerates along a horizontal frictionless surface as the spring returns to its original length. The block leaves the end of the spring with a speed of 2.3 m.s–1, as shown in figure.
The block is released and accelerates along a horizontal frictionless surface as the spring returns to its original length. The block leaves the end of the spring with a speed of 2.3 m.s–1, as shown in figure. The block has a mass of 250 g and the spring has a spring constant of 420 N.m–1. Assume that the spring always obeys Hooke’s law and that all the elastic potential energy of the spring is transferred to the kinetic energy of the block.
The block has a mass of 250 g and the spring has a spring constant of 420 N.m–1. Assume that the spring always obeys Hooke’s law and that all the elastic potential energy of the spring is transferred to the kinetic energy of the block.
a. Calculate the kinetic energy of the block as it leaves the spring.
b. Calculate the compression of the spring immediately before the block is released.
c. After leaving the spring, the block moves along the surface until it hits a barrier at a speed of 2.3 m.s–1. The block then rebounds at a speed of 1.5 m.s–1 and moves back along its original path. The block is in contact with the barrier for a time of 0.086 s.
Calculate:
i. The change in momentum of the block during the collision.
ii. The average resultant force exerted on the block during the collision.
d. The maximum compression x of the spring is now varied in order to vary the kinetic energy EK of the block as it leaves the spring. Assume that all the elastic potential energy in the spring is always transferred to the kinetic energy of the block.
On figure, sketch a graph to show the variation with x of EK
Question 19
A block is pulled by a force X in a straight line along a rough horizontal surface, as shown in figure. Assume that the total resistive force opposing the motion of the block is 0.80 N at all speeds of the block.
Assume that the total resistive force opposing the motion of the block is 0.80 N at all speeds of the block.
The variation with time t of the magnitude of the force X is shown in figure. a. i. Define force.
a. i. Define force.
ii. Determine the change in momentum of the block from time t = 0 to time t = 3.0 s.
b. i. Describe and explain the motion of the block between time t = 3.0 s and time t = 6.0 s.
ii. Force X produces a total power of 2.0 W when moving the block between time t = 3.0 s and time t = 6.0 s.
Calculate the distance moved by the block during this time interval.
c. The block is at rest at time t = 0.
On figure, sketch a graph to show the variation of the momentum of the block with time t from t = 0 to t = 6.0 s.
Numerical values of momentum are not required.
Question 20
a. State Newton’s first law.
b. A log of mass 450 kg is pulled up a slope by a wire attached to a motor, as shown in figure. The angle that the slope makes with the horizontal is 12°. The frictional force acting on the log is 650 N. The log travels with constant velocity.
The angle that the slope makes with the horizontal is 12°. The frictional force acting on the log is 650 N. The log travels with constant velocity.
i. With reference to the motion of the log, discuss whether the log is in equilibrium.
ii. Calculate the tension in the wire.