Question 1
An aircraft, initially stationary on a runway, takes off with a speed of 85 km.h-1 in a distance of no more than 1.20 km.
What is the minimum constant acceleration necessary for the aircraft?
A. 0.23 m.s−2
B. 0.46 m.s−2
C. 3.0 m.s−2
D. 6.0 m.s−2
Easy
Mark as Complete
Mark Scheme
Question 2
An object is moving with an initial velocity of 4.0 m.s−1 to the right.
The velocity of the object changes so that its final velocity is 3.0 m.s−1 downwards, as shown.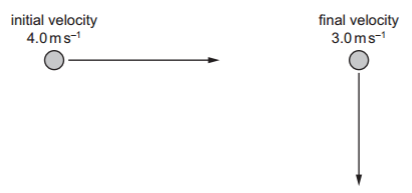 Which arrow represents the change in velocity of the object?
Which arrow represents the change in velocity of the object?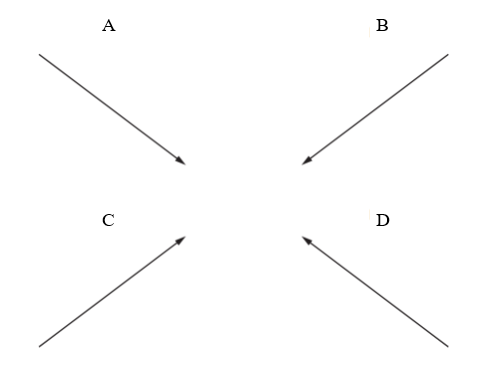
Easy
Mark as Complete
Mark Scheme
Question 3
A car travels anticlockwise along a horizontal circular road of radius 12 m, as shown.
The car takes a time of 4.0 s to move from position P to position Q.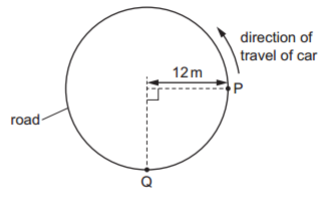 What is the magnitude of the average velocity of the car for the journey from P to Q?
What is the magnitude of the average velocity of the car for the journey from P to Q?
A. 4.2 m.s⁻¹
B. 4.7 m.s⁻¹
C. 6.0 m.s⁻¹
D. 14 m.s⁻¹
Medium
Mark as Complete
Mark Scheme
Question 4
The water surface in a deep well is 78.0 m below the top of the well.
A person at the top of the well drops a heavy stone down the well.
Air resistance is negligible. The speed of sound in the air is 330 m.s⁻¹.
What is the time interval between the person dropping the stone and hearing it hitting the water?
A. 3.75 s
B. 3.99 s
C. 4.19 s
D. 4.22 s
Medium
Mark as Complete
Mark Scheme
Question 5
The graph shows the variation with time `t` of the displacement `s` of an object.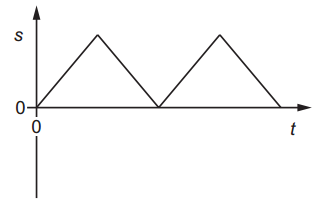 Which graph represents the variation with time `t` of the acceleration `a` of the object?
Which graph represents the variation with time `t` of the acceleration `a` of the object?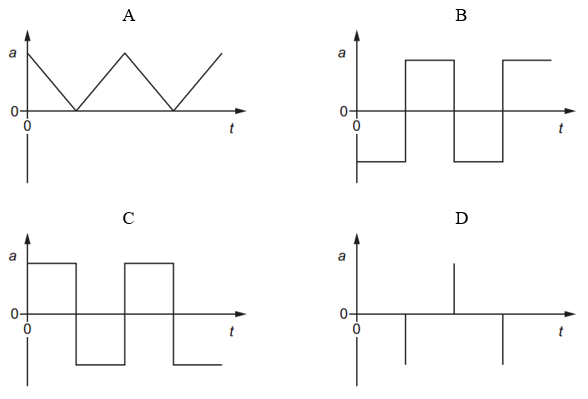
Medium
Mark as Complete
Mark Scheme
Question 6
The velocity–time graphs of four different objects are shown.
Which graph represents an object falling from rest through a long distance in the Earth’s
atmosphere?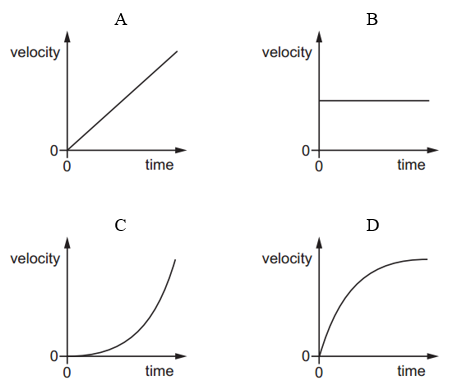
Easy
Mark as Complete
Mark Scheme
Question 7
Which statement is not correct?
A. Acceleration can be determined from the gradient of a velocity–time graph.
B. Acceleration is the rate of change of velocity.
C. Displacement can be determined from the area under a velocity–time graph.
D. Velocity is the rate of change of distance.
Easy
Mark as Complete
Mark Scheme
Question 8
A car travels along a straight horizontal road. The graph shows the variation of the velocity `v` of the car with time `t` for 6.0 s of its journey.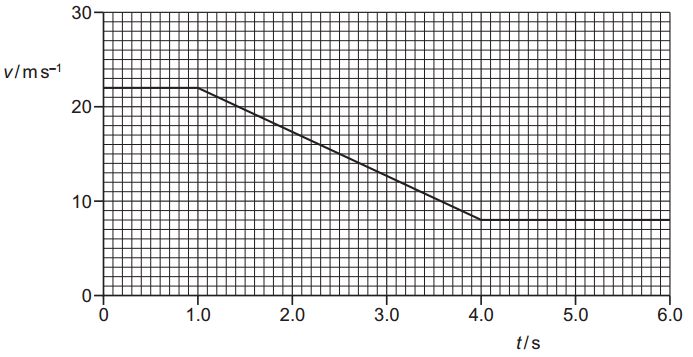 The brakes of the car are applied from t = 1.0 s to t = 4.0 s.
The brakes of the car are applied from t = 1.0 s to t = 4.0 s.
How far does the car travel while the brakes are applied?
A. 21 m
B. 45 m
C. 67 m
D. 83 m
Medium
Mark as Complete
Mark Scheme
Question 9
The graph shows how the acceleration of an object moving in a straight line varies with time.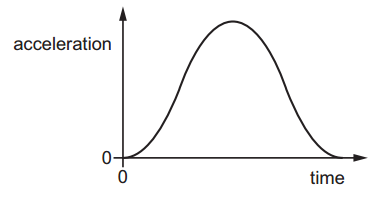 The object starts from rest.
The object starts from rest.
Which graph shows the variation with time of the velocity of the object over the same time interval?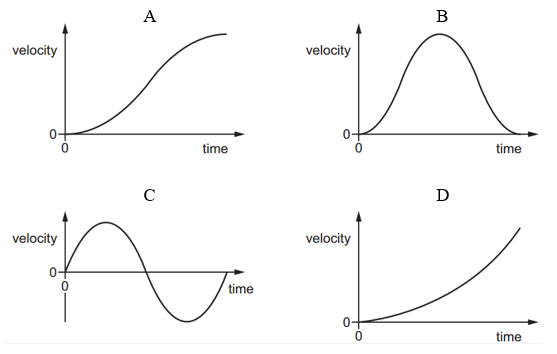
Medium
Mark as Complete
Mark Scheme
Question 10
A rock is launched vertically upwards from the surface of the Earth and an identical rock is launched vertically upwards from the surface of Mars. Each rock is launched with an initial velocity of 12 m.s⁻¹.
Each rock then reaches its maximum height above the surface before returning back down to the surface. The velocity–time graph for each rock is shown. In both cases, air resistance is negligible.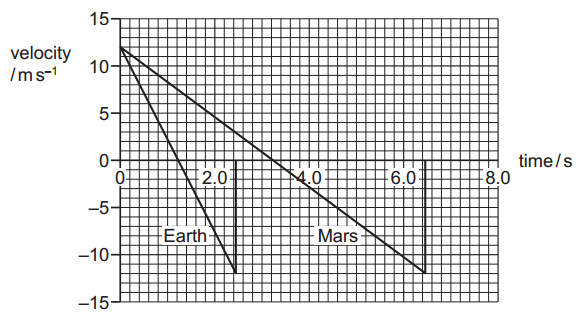 What is the difference in the maximum heights of the two rocks?
What is the difference in the maximum heights of the two rocks?
A. 12 m
B. 15 m
C. 19 m
D. 24 m
Medium
Mark as Complete
Mark Scheme
Question 11
Which graph shows the variation with time `t` of the velocity `v` of an object falling vertically downwards in a vacuum?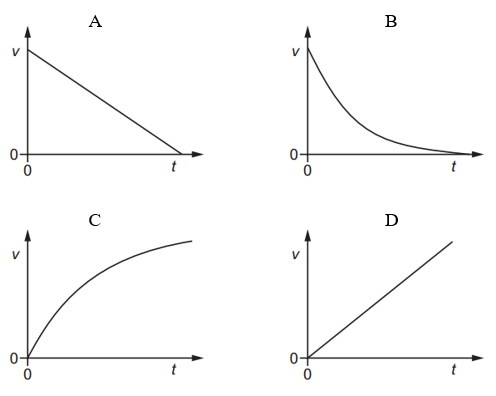
Easy
Mark as Complete
Mark Scheme
Question 12
The graph shows how the velocity v of an object moving in a straight line varies with time t from t = 0 to t = T.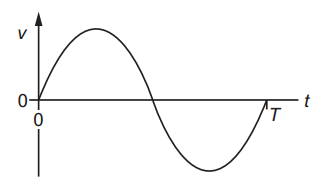 Which graph could represent the displacement s of the object from time t = 0 to t = T?
Which graph could represent the displacement s of the object from time t = 0 to t = T?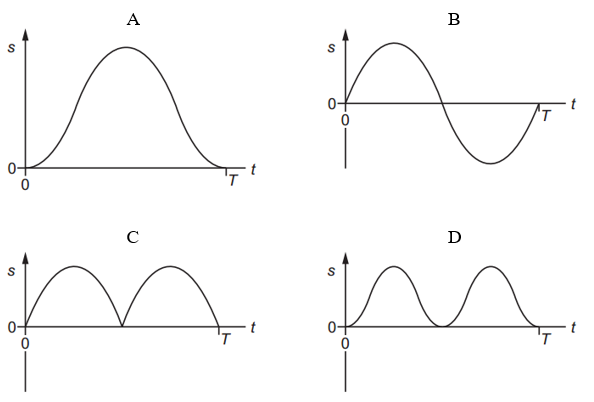
Medium
Mark as Complete
Mark Scheme
Question 13
A goods train passes through a station at a steady speed of 10 m.s–1 at time t = 0. An express train is at rest at the station. The express train leaves the station with a uniform acceleration of 0.5 m.s–2 just as the goods train goes past. Both trains move in the same direction on straight, parallel tracks.
At which time t does the express train overtake the goods train?
A. 6 s
B. 10 s
C. 20 s
D. 40 s
Medium
Mark as Complete
Mark Scheme
Question 14
A stone is thrown vertically upwards from a point X at time t = 0.
The variation with time t of the velocity v of the stone is shown.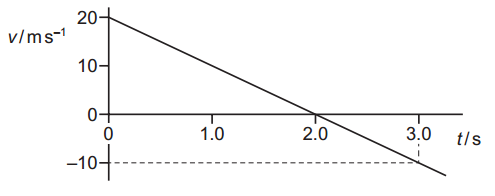 What is the displacement of the stone from point X at time t = 3.0 s?
What is the displacement of the stone from point X at time t = 3.0 s?
A. 15 m above X
B. 15 m below X
C. 25 m above X
D. 25 m below X
Easy
Mark as Complete
Mark Scheme
Question 15
A car X is travelling at a constant speed u along a straight road. At time t = 0 a second car Y is a distance d0 behind car X and travelling at a speed v in the same direction. Speed v is less than speed u.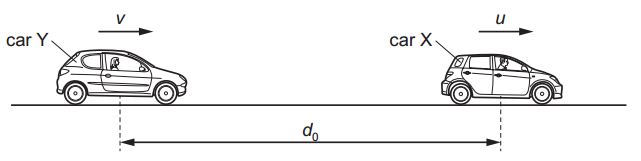 At time t = 0 car Y begins to accelerate with a constant acceleration.
At time t = 0 car Y begins to accelerate with a constant acceleration.
Car Y overtakes car X at time t = T.
Which graph could best show the variation with time t of the distance d between the cars?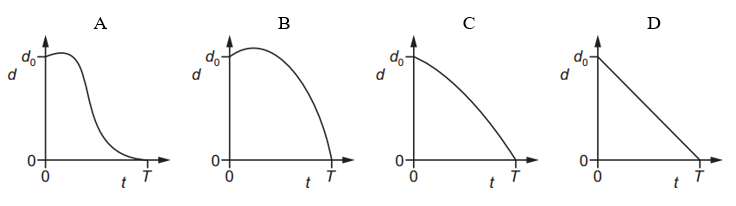
Medium
Mark as Complete
Mark Scheme
Question 16
A skydiver jumps from an aircraft at time t = 0 and falls vertically downwards. The variation with t of her velocity v is shown in figure.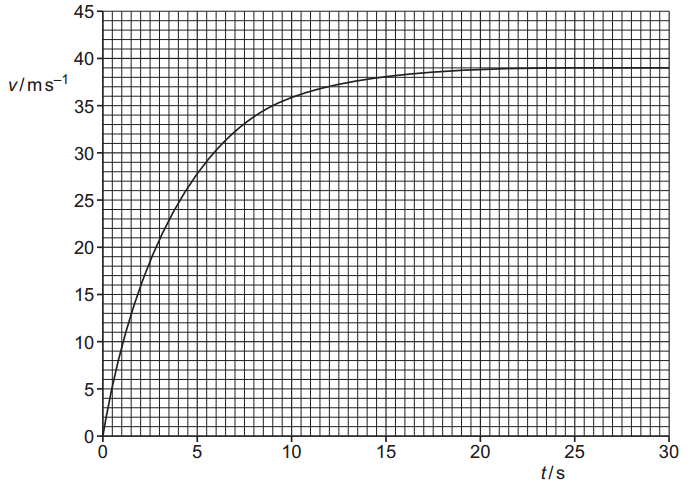
a. i. Using figure, state the terminal velocity of the skydiver.
ii. By drawing a suitable line on figure, determine the acceleration of the skydiver at time t = 9.0 s.
b. The mass of the skydiver and her equipment is 68 kg. The upthrust on the skydiver is negligible.
After reaching terminal velocity, the skydiver opens her parachute at time t1. A total drag force of 1800 N acts on the skydiver.
Determine the magnitude and direction of the acceleration of the skydiver at time t1.
c. The parachute is fully open at time t2. At a later time t3 the skydiver reaches a constant velocity of 5.7 m.s–1.
i. Describe and explain the variation with time of the magnitude of her acceleration between time t2 and time t3.
ii. Calculate the change in momentum of the skydiver between time t1 and time t3.
Medium
Mark as Complete
Mark Scheme
Question 17
a. The distance s moved by an object in time t may be given by the expression `s=1/2at^2`, where a is the acceleration of the object.
State two conditions for this expression to apply to the motion of the object.
b. A student takes a photograph of a steel ball of radius 5.0 cm as it falls from rest. The image of the ball is blurred, as illustrated in figure
The image is blurred because the ball is moving while the photograph is being taken.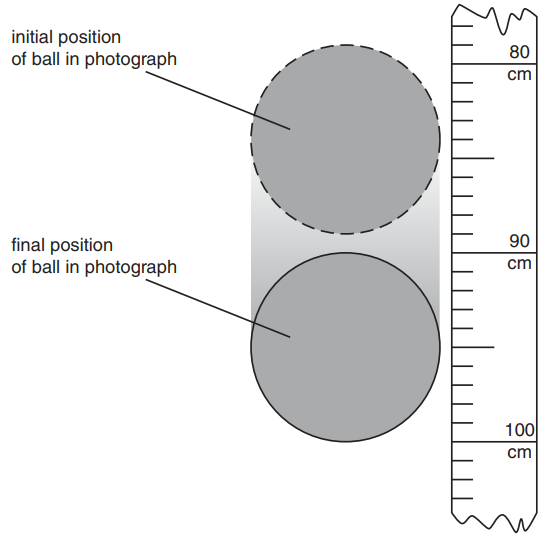 The scale shows the distance fallen from rest by the ball. At time t = 0, the top of the ball is level with the zero mark on the scale. Air resistance is negligible.
The scale shows the distance fallen from rest by the ball. At time t = 0, the top of the ball is level with the zero mark on the scale. Air resistance is negligible.
Calculate:
i. The time the ball falls before the photograph is taken.
ii. The time interval during which the photograph is taken.
c. The student in b. takes a second photograph starting at the same position on the scale.
The ball has the same radius but is less dense, so that air resistance is not negligible.
State and explain the changes that will occur in the photograph.
Hard
Mark as Complete
Mark Scheme
Question 18
A car is travelling along a straight road at speed v. A hazard suddenly appears in front of the car. In the time interval between the hazard appearing and the brakes on the car coming into operation, the car moves forward a distance of 29.3 m. With the brakes applied, the front wheels of the car leave skid marks on the road that are 12.8 m long, as illustrated in figure. It is estimated that, during the skid, the magnitude of the deceleration of the car is 0.85 g, where g is the acceleration of free fall.
It is estimated that, during the skid, the magnitude of the deceleration of the car is 0.85 g, where g is the acceleration of free fall.
a. Determine:
i. The speed v of the car before the brakes are applied.
ii. The time interval between the hazard appearing and the brakes being applied.
b. The legal speed limit on the road is 60 km per hour.
Use both of your answers in a. to comment on the standard of the driving of the car.
Medium
Mark as Complete
Mark Scheme
Question 19
A small ball is thrown horizontally with a speed of 4.0 m.s–1. It falls through a vertical height of 1.96 m before bouncing off a horizontal plate, as illustrated in figure.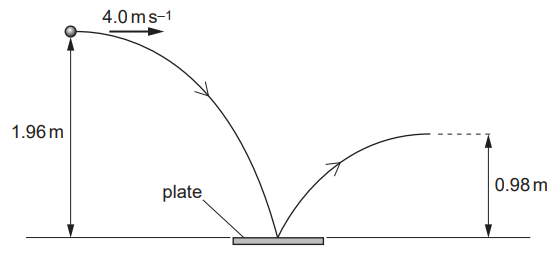 Air resistance is negligible.
Air resistance is negligible.
a. For the ball, as it hits the horizontal plate,
i. State the magnitude of the horizontal component of its velocity.
ii. Show that the vertical component of the velocity is 6.2 m.s–1.
b. The components of the velocity in (a) are both vectors.
Complete figure to draw a vector diagram, to scale, to determine the velocity of the ball as it hits the horizontal plate.![]() c. After bouncing on the plate, the ball rises to a vertical height of 0.98 m.
c. After bouncing on the plate, the ball rises to a vertical height of 0.98 m.
i. Calculate the vertical component of the velocity of the ball as it leaves the plate.
ii. The ball of mass 34 g is in contact with the plate for a time of 0.12 s.
Use your answer in c. i. and the data in a. ii. to calculate, for the ball as it bounces on the plate:
1. The change in momentum
2. The magnitude of the average force exerted by the plate on the ball due to this momentum change.
Hard
Mark as Complete
Mark Scheme
Question 20
a. A ball is thrown vertically down towards the ground and rebounds as illustrated in figure. 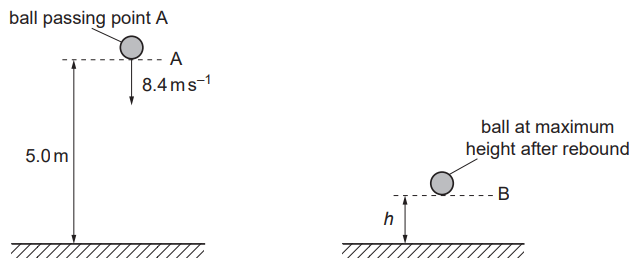 As the ball passes A, it has a speed of 8.4 m.s–1. The height of A is 5.0 m above the ground. The ball hits the ground and rebounds to B. Assume that air resistance is negligible.
As the ball passes A, it has a speed of 8.4 m.s–1. The height of A is 5.0 m above the ground. The ball hits the ground and rebounds to B. Assume that air resistance is negligible.
i. Calculate the speed of the ball as it hits the ground.
ii. Show that the time taken for the ball to reach the ground is 0.47 s.
b. The ball rebounds vertically with a speed of 4.2 m.s–1 as it leaves the ground. The time the ball is in contact with the ground is 20 ms. The ball rebounds to a maximum height h.
The ball passes A at time t = 0. On figure, plot a graph to show the variation with time t of the velocity v of the ball. Continue the graph until the ball has rebounded from the ground and reaches B. c. The ball has a mass of 0.050 kg. It moves from A and reaches B after rebounding.
c. The ball has a mass of 0.050 kg. It moves from A and reaches B after rebounding.
i. For this motion, calculate the change in:
1. Kinetic energy.
2. Gravitational potential energy.
ii. State and explain the total change in energy of the ball for this motion.
Hard
Mark as Complete
Mark Scheme
Question 1
An aircraft, initially stationary on a runway, takes off with a speed of 85 km.h-1 in a distance of no more than 1.20 km.
What is the minimum constant acceleration necessary for the aircraft?
A. 0.23 m.s−2
B. 0.46 m.s−2
C. 3.0 m.s−2
D. 6.0 m.s−2
Answer: A
`v = (85 xx 1000)/3600 = 23.6 " m"."s"^-1`
`v^2 = u^2 + 2 a s`
`a = (v^2 - u^2)/(2 s)= (23.6)^2 / (2 xx 1200) = 556.96 / 2400 = 0.232 " m"."s"^-2`
Question 2
An object is moving with an initial velocity of 4.0 m.s−1 to the right.
The velocity of the object changes so that its final velocity is 3.0 m.s−1 downwards, as shown. Which arrow represents the change in velocity of the object?
Which arrow represents the change in velocity of the object?
Answer: B
`Deltavecv=vecv-vecu=vecv+(-vecu)`
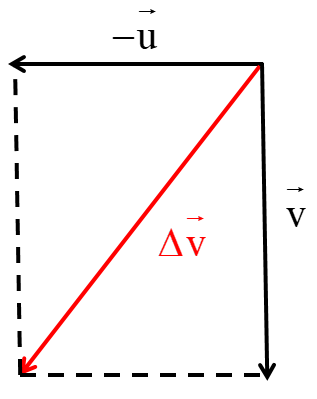
Question 3
A car travels anticlockwise along a horizontal circular road of radius 12 m, as shown.
The car takes a time of 4.0 s to move from position P to position Q. What is the magnitude of the average velocity of the car for the journey from P to Q?
What is the magnitude of the average velocity of the car for the journey from P to Q?
A. 4.2 m.s⁻¹
B. 4.7 m.s⁻¹
C. 6.0 m.s⁻¹
D. 14 m.s⁻¹
Answer: A
Since the car moves along one-quarter of a circle, and radius r = 12 m , the displacement from P to Q is the diagonal of a quarter circle, which forms the hypotenuse of a right-angled triangle:
`"displacement" = sqrt(12^2 + 12^2) = sqrt(288) ~~ 16.97 " m"`
`v_("avg") = "displacement" / "time"=16.97 / 4.0 = 4.24 " m"."s"^-1`
Question 4
The water surface in a deep well is 78.0 m below the top of the well.
A person at the top of the well drops a heavy stone down the well.
Air resistance is negligible. The speed of sound in the air is 330 m.s⁻¹.
What is the time interval between the person dropping the stone and hearing it hitting the water?
A. 3.75 s
B. 3.99 s
C. 4.19 s
D. 4.22 s
Answer: D
`t_("total") = t_1 + t_2`, in which:
Time `t_1` it takes for the stone to fall.
Time `t_2` it takes for the sound to travel back up the well.
Time for the stone to fall: `t_1 = sqrt((2s)/g)= sqrt((2 xx 78.0) / 9.8) = sqrt(15.918) = 3.99 " s"`
Time for the sound to travel back up: `t_2 = "distance"/"speed of sound" = 78.0 / 330 = 0.236 " s"`
Total time interval: `t_("total") = 3.99 + 0.236 = 4.226 ~~ 4.22 " s"`
Question 5
The graph shows the variation with time `t` of the displacement `s` of an object. Which graph represents the variation with time `t` of the acceleration `a` of the object?
Which graph represents the variation with time `t` of the acceleration `a` of the object?
A. Incorrect:
Shows acceleration changing gradually.
But displacement–time graph has straight lines → velocity is constant.
So acceleration should be zero, not changing.
B. Incorrect:
Shows acceleration constantly changing between positive and negative.
That would make a curved displacement graph, not straight lines.
C. Incorrect:
Like B, shows constant acceleration.
But the object moves at constant speed in each part → acceleration should be zero except at turns.
D. Correct:
Acceleration is zero most of the time.
Sharp spikes appear when the object changes direction suddenly.
This matches the displacement graph: straight lines with sudden reversals.
Question 6
The velocity–time graphs of four different objects are shown.
Which graph represents an object falling from rest through a long distance in the Earth’s
atmosphere?
Answer: D
A. Incorrect:
Shows velocity increasing at a constant rate (straight line).
This means constant acceleration (like free fall without air).
But in the atmosphere, air resistance slows the object down.
B. Incorrect:
Shows constant velocity from the start.
That means no acceleration, which doesn’t match an object just starting to fall.
C. Incorrect:
Velocity keeps increasing faster and faster.
That means increasing acceleration, which isn’t correct when air resistance is present.
D. Correct:
Velocity increases quickly at first, then levels off.
This matches an object falling with air resistance — it reaches terminal velocity.
This is the real motion for falling through air over a long distance.
Question 7
Which statement is not correct?
A. Acceleration can be determined from the gradient of a velocity–time graph.
B. Acceleration is the rate of change of velocity.
C. Displacement can be determined from the area under a velocity–time graph.
D. Velocity is the rate of change of distance.
A. Inorrect:
Acceleration is the gradient (slope) of a velocity–time graph.
This shows how fast velocity changes.
So this statement is true.
B. Inorrect:
This is the definition of acceleration.
Acceleration = change in velocity ÷ time.
C. Inorrect:
On a velocity–time graph, the area under the line gives displacement.
This is because velocity × time = displacement.
D. Correct:
Velocity is the rate of change of displacement, not distance.
Displacement includes direction (it's a vector), distance does not.
So this statement is false
Question 8
A car travels along a straight horizontal road. The graph shows the variation of the velocity `v` of the car with time `t` for 6.0 s of its journey. The brakes of the car are applied from t = 1.0 s to t = 4.0 s.
The brakes of the car are applied from t = 1.0 s to t = 4.0 s.
How far does the car travel while the brakes are applied?
A. 21 m
B. 45 m
C. 67 m
D. 83 m
Answer: B
Trapezium area formula: `"area" = 1/2 (v_1 + v_2) xx (t_2 - t_1)`
`v_1 = 22 " m"."s"^-1 , v_2 = 8" m"."s"^-1, t = 4.0 - 1.0 = 3.0 " s"`
`"Distance" = 1/2xx (22 + 8) xx 3 = 45 " m"`
Question 9
The graph shows how the acceleration of an object moving in a straight line varies with time. The object starts from rest.
The object starts from rest.
Which graph shows the variation with time of the velocity of the object over the same time interval?
Answer: A
A. Correct:
Acceleration starts from 0, increases, then decreases back to 0.
So the object speeds up quickly at first, then more slowly.
This gives a velocity graph that curves upward and flattens out.
B. Incorrect
Velocity rises and falls like a "hill."
That would mean the object speeds up then slows back down to rest.
But the acceleration is always positive, so velocity should keep increasing.
C. Incorrect:
Velocity goes up, then becomes negative.
That means the object changes direction.
But the acceleration is always positive → it can’t reverse direction.
D. Incorrect:
Velocity increases faster and faster (curving upward sharply).
This would happen if acceleration keeps increasing.
But the acceleration graph rises then falls, so velocity shouldn't rise this fast.
Question 10
A rock is launched vertically upwards from the surface of the Earth and an identical rock is launched vertically upwards from the surface of Mars. Each rock is launched with an initial velocity of 12 m.s⁻¹.
Each rock then reaches its maximum height above the surface before returning back down to the surface. The velocity–time graph for each rock is shown. In both cases, air resistance is negligible. What is the difference in the maximum heights of the two rocks?
What is the difference in the maximum heights of the two rocks?
A. 12 m
B. 15 m
C. 19 m
D. 24 m
Answer: A
Acceleration due to gravity for both planets:
Earth: `a_E = (0 - 12)/2 = -6.0 " m"."s"^-2`
Mars: `a_M = (0 - 12)/4 = -3.0 " m"."s"^-2`
Maximum height on Earth: `s_E = -u^2 / (2a)=-144 / (-12) = "12 m"`
Maximum height on Mars: `s_M = -u^2 / (2a)=-144 / (-6) = "24 m"`
The difference in the maximum heights of the two rocks: `24 - 12 = "12 m"`
Question 11
Which graph shows the variation with time `t` of the velocity `v` of an object falling vertically downwards in a vacuum?
Answer: D
A. Incorrect:
This graph shows velocity decreasing.
But when falling, velocity increases because gravity pulls the object down.
B. Incorrect:
This graph shows velocity decreasing and flattening out.
That suggests the object is slowing down.
In a vacuum, there is no air resistance — it should speed up.
C. Incorrect:
Velocity increases but levels off.
That would happen if air resistance is present.
But in a vacuum, there is no air → no terminal velocity.
D. Correct:
Velocity increases at a constant rate (straight line).
That’s exactly what happens when falling with no air resistance.
The object accelerates uniformly due to gravity.
Question 12
The graph shows how the velocity v of an object moving in a straight line varies with time t from t = 0 to t = T. Which graph could represent the displacement s of the object from time t = 0 to t = T?
Which graph could represent the displacement s of the object from time t = 0 to t = T?
Answer: A
A. Correct:
Displacement increases at first when velocity is positive.
It flattens out near the end as the object moves back in the opposite direction.
Ends flat at T, because total displacement is zero.
This matches what we expect from the velocity graph.
B. Incorrect:
Displacement goes below zero, which means the object passed the starting point.
But in the velocity graph, the positive and negative areas cancel → total displacement should be zero, not negative.
C. Incorrect:
Shows the object going forward, suddenly dropping to zero, then repeating.
This suggests the object returns to the same point quickly and repeatedly.
That doesn’t match smooth velocity change from the graph.
D. Incorrect:
Displacement increases in two curves.
But it never slows down or levels out.
The object in the velocity graph changes direction, so this graph is not realistic.
Question 13
A goods train passes through a station at a steady speed of 10 m.s–1 at time t = 0. An express train is at rest at the station. The express train leaves the station with a uniform acceleration of 0.5 m.s–2 just as the goods train goes past. Both trains move in the same direction on straight, parallel tracks.
At which time t does the express train overtake the goods train?
A. 6 s
B. 10 s
C. 20 s
D. 40 s
Answer: D
Displacement of goods train: `s =vt= 10 t`
Displacement of express train: `s =1/2xxaxxt^2= 1/2 xx 0.5 xx t^2 = 0.25 t^2`
Set the displacements equal: `10t = 0.25t^2 -> t = "40 s"`
Question 14
A stone is thrown vertically upwards from a point X at time t = 0.
The variation with time t of the velocity v of the stone is shown. What is the displacement of the stone from point X at time t = 3.0 s?
What is the displacement of the stone from point X at time t = 3.0 s?
A. 15 m above X
B. 15 m below X
C. 25 m above X
D. 25 m below X
Answer: A
Upward displacement (0 to 2.0 s): `s_1 = 1/2 xx 2.0 xx 20 = "20 m"`
Downward displacement (2.0 to 3.0 s): `s_2 = 1/2 xx 1.0 xx 10 = "5 m"`
Total displacement: `s = 20 - 5 = "15 m"`
Question 15
A car X is travelling at a constant speed u along a straight road. At time t = 0 a second car Y is a distance d0 behind car X and travelling at a speed v in the same direction. Speed v is less than speed u. At time t = 0 car Y begins to accelerate with a constant acceleration.
At time t = 0 car Y begins to accelerate with a constant acceleration.
Car Y overtakes car X at time t = T.
Which graph could best show the variation with time t of the distance d between the cars?
Answer: B
A. Incorrect:
The gap suddenly drops at the start, which suggests car Y was always faster.
But at t = 0, car Y is slower than car X.
So the distance should increase at first, not decrease.
B. Correct:
Distance first increases (because Y starts slower).
Then car Y speeds up (due to constant acceleration), closes the gap, and overtakes car X at time .
The curve shape matches that: rise, then fall to zero.
C. Incorrect:
Shows the distance decreasing constantly like a straight line.
That would happen if Y had higher constant speed, not constant acceleration.
But Y starts slower, so the curve must rise first.
D. Incorrect:
Shows a steady linear drop.
Again, suggests equal rate of closing the gap, not realistic for accelerating motion.
Question 16
A skydiver jumps from an aircraft at time t = 0 and falls vertically downwards. The variation with t of her velocity v is shown in figure.
a. i. Using figure, state the terminal velocity of the skydiver.
ii. By drawing a suitable line on figure, determine the acceleration of the skydiver at time t = 9.0 s.
b. The mass of the skydiver and her equipment is 68 kg. The upthrust on the skydiver is negligible.
After reaching terminal velocity, the skydiver opens her parachute at time t1. A total drag force of 1800 N acts on the skydiver.
Determine the magnitude and direction of the acceleration of the skydiver at time t1.
c. The parachute is fully open at time t2. At a later time t3 the skydiver reaches a constant velocity of 5.7 m.s–1.
i. Describe and explain the variation with time of the magnitude of her acceleration between time t2 and time t3.
ii. Calculate the change in momentum of the skydiver between time t1 and time t3.
a. i. From the graph, the velocity levels off at around 39 m.s-1.
Terminal velocity = 39 m.s-1.
ii. Draw a tangent line to the curve at t = 9.0 s.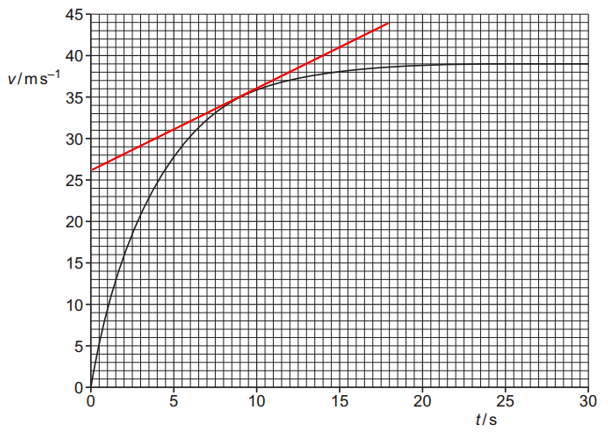
`a =(Delta v) / (Delta t) =(44-26)/(18-0) =18 / 18 = 1.0 " m"."s"^-2`
b. `W = m g = 68 xx 9.81 = "667.08 N"`
`F_("net") = 667.08 - 1800 = -1132.92 " N"`
`a = F/m = -1132.92 / 68 ~~ -17 " m"."s"^-2`
Direction: Upwards (because net force is upward).
c. i. After the parachute opens, speed decreases, so drag force decreases.
As drag decreases, the net force becomes smaller, so acceleration decreases.
When drag balances weight again, acceleration becomes zero → terminal velocity is reached again.
ii. `Delta p = m (v - u) = 68xx (5.7 - 39) = 68 xx (-33.3) = -2264.4 " Ns"`
Question 17
a. The distance s moved by an object in time t may be given by the expression `s=1/2at^2`, where a is the acceleration of the object.
State two conditions for this expression to apply to the motion of the object.
b. A student takes a photograph of a steel ball of radius 5.0 cm as it falls from rest. The image of the ball is blurred, as illustrated in figure
The image is blurred because the ball is moving while the photograph is being taken. The scale shows the distance fallen from rest by the ball. At time t = 0, the top of the ball is level with the zero mark on the scale. Air resistance is negligible.
The scale shows the distance fallen from rest by the ball. At time t = 0, the top of the ball is level with the zero mark on the scale. Air resistance is negligible.
Calculate:
i. The time the ball falls before the photograph is taken.
ii. The time interval during which the photograph is taken.
c. The student in b. takes a second photograph starting at the same position on the scale.
The ball has the same radius but is less dense, so that air resistance is not negligible.
State and explain the changes that will occur in the photograph.
a. The object must start from rest (initial speed = 0).
The acceleration must be constant and in a straight line.
b. i. `t = sqrt((2s)/g)= sqrt((2 xx 0.79)/9.8) = sqrt(0.1612) = 0.40 "s"`
ii. `Deltat=sqrt((2xx0.9)/(9.8))-sqrt((2xx0.79)/(9.8))="0.03 s"`
c. Change: The blurred image of the ball will be shorter.
Explanation: Air resistance causes the ball to fall more slowly and with lower acceleration, so it travels less distance during the same time.
Question 18
A car is travelling along a straight road at speed v. A hazard suddenly appears in front of the car. In the time interval between the hazard appearing and the brakes on the car coming into operation, the car moves forward a distance of 29.3 m. With the brakes applied, the front wheels of the car leave skid marks on the road that are 12.8 m long, as illustrated in figure. It is estimated that, during the skid, the magnitude of the deceleration of the car is 0.85 g, where g is the acceleration of free fall.
It is estimated that, during the skid, the magnitude of the deceleration of the car is 0.85 g, where g is the acceleration of free fall.
a. Determine:
i. The speed v of the car before the brakes are applied.
ii. The time interval between the hazard appearing and the brakes being applied.
b. The legal speed limit on the road is 60 km per hour.
Use both of your answers in a. to comment on the standard of the driving of the car.
a. i. `v = sqrt(2a s)=sqrt(2 xx 8.33 xx 12.8) = sqrt(213.25) = 14.6 " m"."s"^-1`
ii. The car travels 29.3 m at constant speed (no braking yet), so:
`t = d / v = 29.3 / 14.6 = "2.0 s"`
b. Legal speed limit = 60 km.h-1 = 16.7 m.s-1.
The driver’s speed is 14.6 m.s-1.
Speed is within legal limit.
But reaction time is too long, suggesting poor driving standard.
Question 19
A small ball is thrown horizontally with a speed of 4.0 m.s–1. It falls through a vertical height of 1.96 m before bouncing off a horizontal plate, as illustrated in figure. Air resistance is negligible.
Air resistance is negligible.
a. For the ball, as it hits the horizontal plate,
i. State the magnitude of the horizontal component of its velocity.
ii. Show that the vertical component of the velocity is 6.2 m.s–1.
b. The components of the velocity in (a) are both vectors.
Complete figure to draw a vector diagram, to scale, to determine the velocity of the ball as it hits the horizontal plate.![]() c. After bouncing on the plate, the ball rises to a vertical height of 0.98 m.
c. After bouncing on the plate, the ball rises to a vertical height of 0.98 m.
i. Calculate the vertical component of the velocity of the ball as it leaves the plate.
ii. The ball of mass 34 g is in contact with the plate for a time of 0.12 s.
Use your answer in c. i. and the data in a. ii. to calculate, for the ball as it bounces on the plate:
1. The change in momentum
2. The magnitude of the average force exerted by the plate on the ball due to this momentum change.
a. i. Since air resistance is negligible, horizontal velocity remains constant.
`v_("horizontal") = 4.0 " m"."s"^-1`
ii. Since the ball falls from rest vertically: u = 0
`v = sqrt(2 xx 9.8 xx 1.96) = sqrt(38.416) = 6.2 " m"."s"^-1`
b. Since `v_xbotv_y`
Resultant velocity of the ball: `v = sqrt(4.0^2 + 6.2^2) = sqrt(54.44) = 7.4 " m"."s"^-1`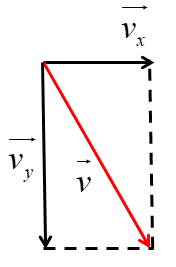 `theta = tan^-1(4.0 / 6.2) = 33^@ "to vertical"`
`theta = tan^-1(4.0 / 6.2) = 33^@ "to vertical"`
c. i. Vertical component of the velocity as it leaves the plate:
`v = sqrt(2 xx 9.8 xx 0.98) = sqrt(19.208) = 4.4 " m"."s"^-1`
ii. Change in vertical momentum: `Delta p = 0.034 xx (4.4 - (- 6.2)) = 0.36 " kg"."m"."s"^-1`
`F = (Delta p) / (Delta t) = 0.36 / 0.12 = "3.0 N"`
Question 20
a. A ball is thrown vertically down towards the ground and rebounds as illustrated in figure. 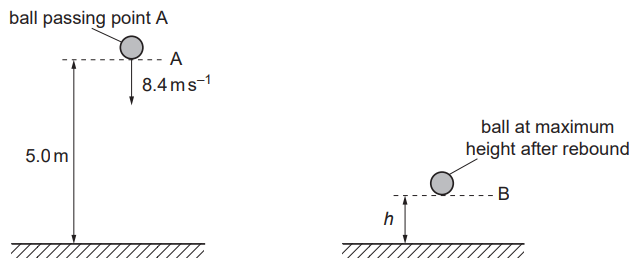 As the ball passes A, it has a speed of 8.4 m.s–1. The height of A is 5.0 m above the ground. The ball hits the ground and rebounds to B. Assume that air resistance is negligible.
As the ball passes A, it has a speed of 8.4 m.s–1. The height of A is 5.0 m above the ground. The ball hits the ground and rebounds to B. Assume that air resistance is negligible.
i. Calculate the speed of the ball as it hits the ground.
ii. Show that the time taken for the ball to reach the ground is 0.47 s.
b. The ball rebounds vertically with a speed of 4.2 m.s–1 as it leaves the ground. The time the ball is in contact with the ground is 20 ms. The ball rebounds to a maximum height h.
The ball passes A at time t = 0. On figure, plot a graph to show the variation with time t of the velocity v of the ball. Continue the graph until the ball has rebounded from the ground and reaches B. c. The ball has a mass of 0.050 kg. It moves from A and reaches B after rebounding.
c. The ball has a mass of 0.050 kg. It moves from A and reaches B after rebounding.
i. For this motion, calculate the change in:
1. Kinetic energy.
2. Gravitational potential energy.
ii. State and explain the total change in energy of the ball for this motion.
a. i. Speed of ball as it hits the ground:
`v = sqrt(u^2+2as)= sqrt((8.4)^2 + 2 xx 9.81 xx 5.0) = sqrt(168.66) = 13.0 " m"."s"^-1`
ii. `t = (v-u)/a= (13.0 - 8.4) / 9.81 = "0.47 s"`
b. 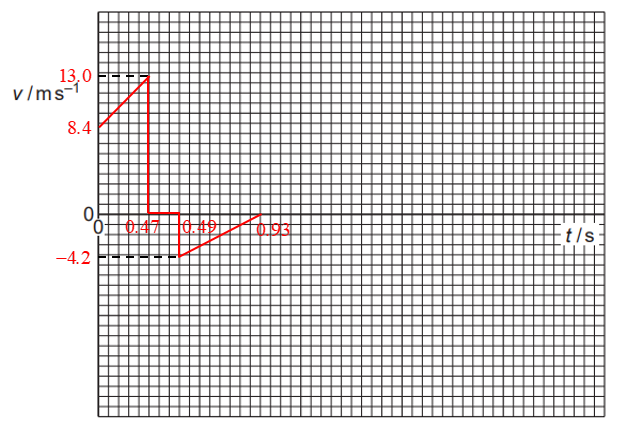
c. i. 1. `Delta KE = 1/2mv_B^2-1/2mv_A^2= 0 - 0.5 xx 0.050 xx (8.4)^2 = -1.8 " J"`
2. `Delta PE =mgh= 0.050 xx 9.8 xx (0.9 - 5.0) = -2.0 " J"`
`h = v^2/(2g)= (4.2)^2 / (2 xx 9.8) = "0.9 m"`
ii. Total energy change = `-3.8 " J"`
Energy is lost due to: deformation on impact, heat/sound generated.
Question 1
An aircraft, initially stationary on a runway, takes off with a speed of 85 km.h-1 in a distance of no more than 1.20 km.
What is the minimum constant acceleration necessary for the aircraft?
A. 0.23 m.s−2
B. 0.46 m.s−2
C. 3.0 m.s−2
D. 6.0 m.s−2
Question 2
An object is moving with an initial velocity of 4.0 m.s−1 to the right.
The velocity of the object changes so that its final velocity is 3.0 m.s−1 downwards, as shown. Which arrow represents the change in velocity of the object?
Which arrow represents the change in velocity of the object?
Question 3
A car travels anticlockwise along a horizontal circular road of radius 12 m, as shown.
The car takes a time of 4.0 s to move from position P to position Q. What is the magnitude of the average velocity of the car for the journey from P to Q?
What is the magnitude of the average velocity of the car for the journey from P to Q?
A. 4.2 m.s⁻¹
B. 4.7 m.s⁻¹
C. 6.0 m.s⁻¹
D. 14 m.s⁻¹
Question 4
The water surface in a deep well is 78.0 m below the top of the well.
A person at the top of the well drops a heavy stone down the well.
Air resistance is negligible. The speed of sound in the air is 330 m.s⁻¹.
What is the time interval between the person dropping the stone and hearing it hitting the water?
A. 3.75 s
B. 3.99 s
C. 4.19 s
D. 4.22 s
Question 5
The graph shows the variation with time `t` of the displacement `s` of an object. Which graph represents the variation with time `t` of the acceleration `a` of the object?
Which graph represents the variation with time `t` of the acceleration `a` of the object?
Question 6
The velocity–time graphs of four different objects are shown.
Which graph represents an object falling from rest through a long distance in the Earth’s
atmosphere?
Question 7
Which statement is not correct?
A. Acceleration can be determined from the gradient of a velocity–time graph.
B. Acceleration is the rate of change of velocity.
C. Displacement can be determined from the area under a velocity–time graph.
D. Velocity is the rate of change of distance.
Question 8
A car travels along a straight horizontal road. The graph shows the variation of the velocity `v` of the car with time `t` for 6.0 s of its journey. The brakes of the car are applied from t = 1.0 s to t = 4.0 s.
The brakes of the car are applied from t = 1.0 s to t = 4.0 s.
How far does the car travel while the brakes are applied?
A. 21 m
B. 45 m
C. 67 m
D. 83 m
Question 9
The graph shows how the acceleration of an object moving in a straight line varies with time. The object starts from rest.
The object starts from rest.
Which graph shows the variation with time of the velocity of the object over the same time interval?
Question 10
A rock is launched vertically upwards from the surface of the Earth and an identical rock is launched vertically upwards from the surface of Mars. Each rock is launched with an initial velocity of 12 m.s⁻¹.
Each rock then reaches its maximum height above the surface before returning back down to the surface. The velocity–time graph for each rock is shown. In both cases, air resistance is negligible. What is the difference in the maximum heights of the two rocks?
What is the difference in the maximum heights of the two rocks?
A. 12 m
B. 15 m
C. 19 m
D. 24 m
Question 11
Which graph shows the variation with time `t` of the velocity `v` of an object falling vertically downwards in a vacuum?
Question 12
The graph shows how the velocity v of an object moving in a straight line varies with time t from t = 0 to t = T. Which graph could represent the displacement s of the object from time t = 0 to t = T?
Which graph could represent the displacement s of the object from time t = 0 to t = T?
Question 13
A goods train passes through a station at a steady speed of 10 m.s–1 at time t = 0. An express train is at rest at the station. The express train leaves the station with a uniform acceleration of 0.5 m.s–2 just as the goods train goes past. Both trains move in the same direction on straight, parallel tracks.
At which time t does the express train overtake the goods train?
A. 6 s
B. 10 s
C. 20 s
D. 40 s
Question 14
A stone is thrown vertically upwards from a point X at time t = 0.
The variation with time t of the velocity v of the stone is shown. What is the displacement of the stone from point X at time t = 3.0 s?
What is the displacement of the stone from point X at time t = 3.0 s?
A. 15 m above X
B. 15 m below X
C. 25 m above X
D. 25 m below X
Question 15
A car X is travelling at a constant speed u along a straight road. At time t = 0 a second car Y is a distance d0 behind car X and travelling at a speed v in the same direction. Speed v is less than speed u. At time t = 0 car Y begins to accelerate with a constant acceleration.
At time t = 0 car Y begins to accelerate with a constant acceleration.
Car Y overtakes car X at time t = T.
Which graph could best show the variation with time t of the distance d between the cars?
Question 16
A skydiver jumps from an aircraft at time t = 0 and falls vertically downwards. The variation with t of her velocity v is shown in figure.
a. i. Using figure, state the terminal velocity of the skydiver.
ii. By drawing a suitable line on figure, determine the acceleration of the skydiver at time t = 9.0 s.
b. The mass of the skydiver and her equipment is 68 kg. The upthrust on the skydiver is negligible.
After reaching terminal velocity, the skydiver opens her parachute at time t1. A total drag force of 1800 N acts on the skydiver.
Determine the magnitude and direction of the acceleration of the skydiver at time t1.
c. The parachute is fully open at time t2. At a later time t3 the skydiver reaches a constant velocity of 5.7 m.s–1.
i. Describe and explain the variation with time of the magnitude of her acceleration between time t2 and time t3.
ii. Calculate the change in momentum of the skydiver between time t1 and time t3.
Question 17
a. The distance s moved by an object in time t may be given by the expression `s=1/2at^2`, where a is the acceleration of the object.
State two conditions for this expression to apply to the motion of the object.
b. A student takes a photograph of a steel ball of radius 5.0 cm as it falls from rest. The image of the ball is blurred, as illustrated in figure
The image is blurred because the ball is moving while the photograph is being taken. The scale shows the distance fallen from rest by the ball. At time t = 0, the top of the ball is level with the zero mark on the scale. Air resistance is negligible.
The scale shows the distance fallen from rest by the ball. At time t = 0, the top of the ball is level with the zero mark on the scale. Air resistance is negligible.
Calculate:
i. The time the ball falls before the photograph is taken.
ii. The time interval during which the photograph is taken.
c. The student in b. takes a second photograph starting at the same position on the scale.
The ball has the same radius but is less dense, so that air resistance is not negligible.
State and explain the changes that will occur in the photograph.
Question 18
A car is travelling along a straight road at speed v. A hazard suddenly appears in front of the car. In the time interval between the hazard appearing and the brakes on the car coming into operation, the car moves forward a distance of 29.3 m. With the brakes applied, the front wheels of the car leave skid marks on the road that are 12.8 m long, as illustrated in figure. It is estimated that, during the skid, the magnitude of the deceleration of the car is 0.85 g, where g is the acceleration of free fall.
It is estimated that, during the skid, the magnitude of the deceleration of the car is 0.85 g, where g is the acceleration of free fall.
a. Determine:
i. The speed v of the car before the brakes are applied.
ii. The time interval between the hazard appearing and the brakes being applied.
b. The legal speed limit on the road is 60 km per hour.
Use both of your answers in a. to comment on the standard of the driving of the car.
Question 19
A small ball is thrown horizontally with a speed of 4.0 m.s–1. It falls through a vertical height of 1.96 m before bouncing off a horizontal plate, as illustrated in figure. Air resistance is negligible.
Air resistance is negligible.
a. For the ball, as it hits the horizontal plate,
i. State the magnitude of the horizontal component of its velocity.
ii. Show that the vertical component of the velocity is 6.2 m.s–1.
b. The components of the velocity in (a) are both vectors.
Complete figure to draw a vector diagram, to scale, to determine the velocity of the ball as it hits the horizontal plate.![]() c. After bouncing on the plate, the ball rises to a vertical height of 0.98 m.
c. After bouncing on the plate, the ball rises to a vertical height of 0.98 m.
i. Calculate the vertical component of the velocity of the ball as it leaves the plate.
ii. The ball of mass 34 g is in contact with the plate for a time of 0.12 s.
Use your answer in c. i. and the data in a. ii. to calculate, for the ball as it bounces on the plate:
1. The change in momentum
2. The magnitude of the average force exerted by the plate on the ball due to this momentum change.
Question 20
a. A ball is thrown vertically down towards the ground and rebounds as illustrated in figure. 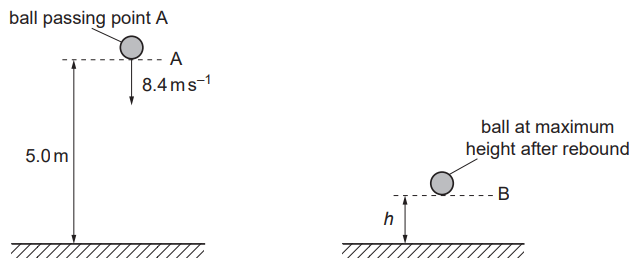 As the ball passes A, it has a speed of 8.4 m.s–1. The height of A is 5.0 m above the ground. The ball hits the ground and rebounds to B. Assume that air resistance is negligible.
As the ball passes A, it has a speed of 8.4 m.s–1. The height of A is 5.0 m above the ground. The ball hits the ground and rebounds to B. Assume that air resistance is negligible.
i. Calculate the speed of the ball as it hits the ground.
ii. Show that the time taken for the ball to reach the ground is 0.47 s.
b. The ball rebounds vertically with a speed of 4.2 m.s–1 as it leaves the ground. The time the ball is in contact with the ground is 20 ms. The ball rebounds to a maximum height h.
The ball passes A at time t = 0. On figure, plot a graph to show the variation with time t of the velocity v of the ball. Continue the graph until the ball has rebounded from the ground and reaches B. c. The ball has a mass of 0.050 kg. It moves from A and reaches B after rebounding.
c. The ball has a mass of 0.050 kg. It moves from A and reaches B after rebounding.
i. For this motion, calculate the change in:
1. Kinetic energy.
2. Gravitational potential energy.
ii. State and explain the total change in energy of the ball for this motion.