Question 1
A stationary (standing) wave is set up on a vibrating spring. Adjacent nodes are separated by 25 cm. Calculate:
a. The wavelength of the progressive wave.
b. The distance from a node to an adjacent antinode.
Easy
Mark as Complete
Mark Scheme
Question 2
A string is fixed between points X and Y.
A stationary wave pattern is formed on the stretched string. 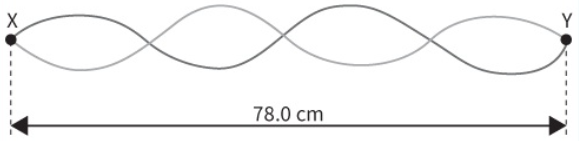 The distance between X and Y is 78 cm. The string vibrates at a frequency of 120 Hz. What is the speed of the progressive wave on the string?
The distance between X and Y is 78 cm. The string vibrates at a frequency of 120 Hz. What is the speed of the progressive wave on the string?
Easy
Mark as Complete
Mark Scheme
Question 3
Find the fundamental frequency and next two possible resonant frequencies for an organ pipe which is 0.17 m long and closed at one end. The speed of sound in air is 340 m.s–1.
Medium
Mark as Complete
Mark Scheme
Question 4
A vibrating tuning fork of frequency 320 Hz is held over the open end of a resonance tube. The other end of the tube is immersed in water. The length of the air column is gradually increased until resonance first occurs. Taking the speed of sound in air as 340 m.s–1, calculate the length of the air column.
Medium
Mark as Complete
Mark Scheme
Question 5
A long glass tube is almost completely immersed in a large tank of water. A tuning fork is struck and held just above the open end of the tube as it is slowly raised.
A louder sound is first heard when the height h of the end of the tube above the water is 18.8 cm.
A louder sound is next heard when h is 56.4 cm.
The speed of sound in air is 330 m.s-1.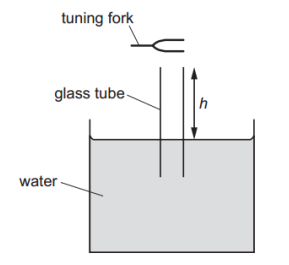 What is the frequency of the sound produced by the tuning fork?
What is the frequency of the sound produced by the tuning fork?
Medium
Mark as Complete
Mark Scheme
Question 6
A speaker is set up at the open end of a closed tube containing powder.
When the speaker produces sound of frequency 1200 Hz, a stationary wave is produced in the tube.
The powder gathers at the nodes of the stationary wave as shown in the diagram.
The speed of sound in air is 336 m.s-1. What is the value of distance x?
What is the value of distance x?
Medium
Mark as Complete
Mark Scheme
Question 7
A vertical tube is partially filled with water. A sound wave moves down the tube and is reflected by the surface of the water.
The frequency of the sound wave is gradually increased from zero until a much louder sound is heard.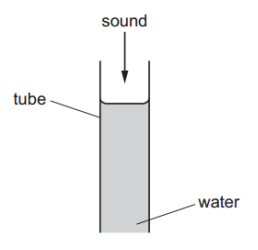 Water is then removed from the tube until a second louder sound is heard.
Water is then removed from the tube until a second louder sound is heard.
Which diagram shows the new pattern of the stationary wave that is formed?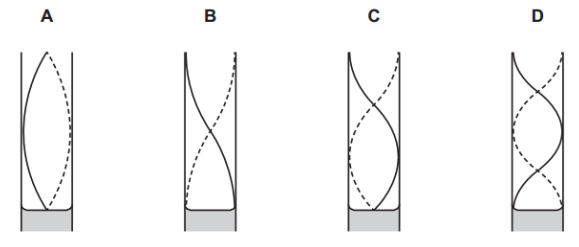
Medium
Mark as Complete
Mark Scheme
Question 8
The diagram shows part of a stationary wave on a string.
X and Y are points on the string. The vibrations at X and Y are 180° out of phase.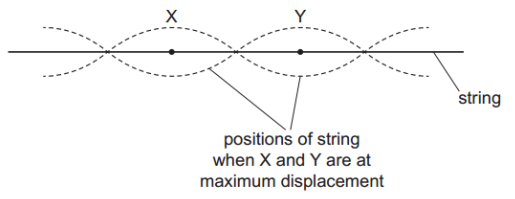 What is the distance between X and Y?
What is the distance between X and Y?
A. One-quarter of a wavelength.
B. Half a wavelength.
C. One wavelength.
D. Two wavelengths.
Medium
Mark as Complete
Mark Scheme
Question 9
A pipe of length L is open at one end and closed at the other. A loudspeaker is at the open end and emits a sound wave into the pipe.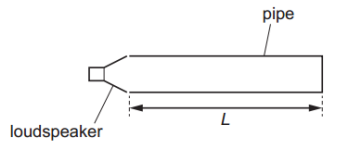
When a stationary wave is formed, there is an antinode at the open end of the pipe.
Which wavelength of sound could be used to produce a stationary wave?
A. `(2L)/3`
B. `L`
C. `(4L)/3`
D. `2L`
Hard
Mark as Complete
Mark Scheme
Question 10
A pipe, closed at one end, has a loudspeaker at the open end. For some frequencies of sound from the loudspeaker, a stationary sound wave is formed in the air within the pipe with an antinode at the open end of the pipe.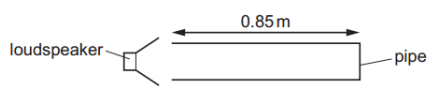 The length of the pipe is 0.85 m.
The length of the pipe is 0.85 m.
The speed of sound in air is 350 m.s-1
Which frequency of sound from the loudspeaker would NOT produce a stationary wave?
A. 100 Hz.
B. 200 Hz.
C. 300 Hz.
D. 500 Hz.
Hard
Mark as Complete
Mark Scheme
Question 1
A stationary (standing) wave is set up on a vibrating spring. Adjacent nodes are separated by 25 cm. Calculate:
a. The wavelength of the progressive wave.
b. The distance from a node to an adjacent antinode.
a. Wavelength of stationary wave = 2 × distance between nodes = 50 cm.
b. Distance from node to adjacent antinode = 0.5 × distance between nodes = 12.5 cm.
Question 2
A string is fixed between points X and Y.
A stationary wave pattern is formed on the stretched string.  The distance between X and Y is 78 cm. The string vibrates at a frequency of 120 Hz. What is the speed of the progressive wave on the string?
The distance between X and Y is 78 cm. The string vibrates at a frequency of 120 Hz. What is the speed of the progressive wave on the string?
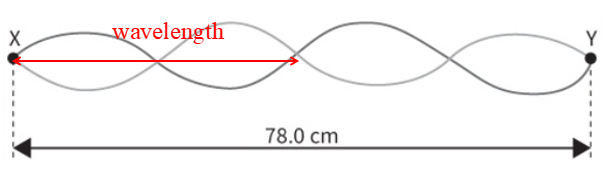 78 cm = 2 λ
78 cm = 2 λ
λ = 39 cm; `v = f xx λ = 120 × 0.39 = 46.8 " m.s"^-1`
Question 3
Find the fundamental frequency and next two possible resonant frequencies for an organ pipe which is 0.17 m long and closed at one end. The speed of sound in air is 340 m.s–1.
The frequencies of the fundamental and next two possible resonant frequencies of a tube of length L, closed at one end, are `f_1 = c/(4L)`, `f_2 = (3c)/(4L)`, `f_3 = (5c)/(4L)`
Fundamental mode (first harmonic) f1:
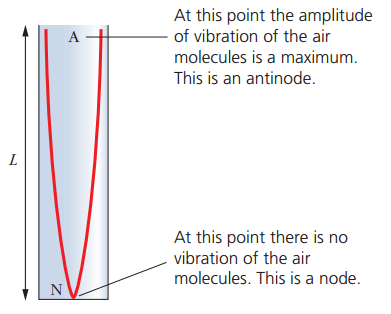 Second harmonic f2:
Second harmonic f2: Third harmonic f3:
Third harmonic f3: The frequencies are thus: 500 Hz, 1500 Hz, and 2500 Hz.
The frequencies are thus: 500 Hz, 1500 Hz, and 2500 Hz.
Question 4
A vibrating tuning fork of frequency 320 Hz is held over the open end of a resonance tube. The other end of the tube is immersed in water. The length of the air column is gradually increased until resonance first occurs. Taking the speed of sound in air as 340 m.s–1, calculate the length of the air column.
The tube is closed at one end (because the other end is in water).
So first resonance occurs at 1/4 of the wavelength: `L = lambda / 4`
`lambda = v / f = 340 / 320 = "1.0625 m"`
`L = lambda / 4 = 1.0625 / 4 ~~ "0.26 m"`
Question 5
A long glass tube is almost completely immersed in a large tank of water. A tuning fork is struck and held just above the open end of the tube as it is slowly raised.
A louder sound is first heard when the height h of the end of the tube above the water is 18.8 cm.
A louder sound is next heard when h is 56.4 cm.
The speed of sound in air is 330 m.s-1. What is the frequency of the sound produced by the tuning fork?
What is the frequency of the sound produced by the tuning fork?
In a closed pipe (open at one end, closed at the other):
First resonance: `L_1 = λ / 4`
Second resonance: `L_2 = (3λ) / 4`
So the difference between the lengths gives: `L_2 - L_1 = (3 lambda) / 4 - lambda / 4 = lambda / 2`
`DeltaL = L_2 - L_1 = 0.564 - 0.188 = "0.376 m"`
`lambda = 2 xx 0.376 = "0.752 m"`
`f = v / lambda = 330 / 0.752 approx "439.4 Hz"`
Question 6
A speaker is set up at the open end of a closed tube containing powder.
When the speaker produces sound of frequency 1200 Hz, a stationary wave is produced in the tube.
The powder gathers at the nodes of the stationary wave as shown in the diagram.
The speed of sound in air is 336 m.s-1. What is the value of distance x?
What is the value of distance x?
`lambda = v / f = 336 / 1200 = "0.28 m"`
The powder gathers at nodes, which are spaced half a wavelength apart in a stationary wave.
So `x = lambda / 2 = 0.28 / 2 = "0.14 m"`
However, the diagram shows three node-to-node distances, meaning:
`x = 3 xx (lambda / 2) = 3 xx 0.14 = "0.42 m"`
Question 7
A vertical tube is partially filled with water. A sound wave moves down the tube and is reflected by the surface of the water.
The frequency of the sound wave is gradually increased from zero until a much louder sound is heard. Water is then removed from the tube until a second louder sound is heard.
Water is then removed from the tube until a second louder sound is heard.
Which diagram shows the new pattern of the stationary wave that is formed?
Answer: C
This is a classic example of a resonance tube with one end closed (at the water surface) and the other end open (at the top).
The first louder sound occurs when the air column supports the first harmonic (fundamental mode). This corresponds to a quarter of a wavelength λ/4 in the tube.
When more water is removed, the air column becomes longer, and the next resonance occurs at the third harmonic, which corresponds to three quarters of a wavelength 3λ/4.
So the new wave pattern should have one more node and one more antinode, forming the third harmonic 3λ/4.
Question 8
The diagram shows part of a stationary wave on a string.
X and Y are points on the string. The vibrations at X and Y are 180° out of phase. What is the distance between X and Y?
What is the distance between X and Y?
A. One-quarter of a wavelength.
B. Half a wavelength.
C. One wavelength.
D. Two wavelengths.
Answer: B
In a stationary wave, points that are 180° out of phase are separated by half of a wavelength.
From the diagram:
X and Y are adjacent antinodes.
In a stationary wave, antinodes (maximum displacement) occur at every half-wavelength.
So, the distance between X and Y is: `x = λ / 2`
Question 9
A pipe of length L is open at one end and closed at the other. A loudspeaker is at the open end and emits a sound wave into the pipe.
When a stationary wave is formed, there is an antinode at the open end of the pipe.
Which wavelength of sound could be used to produce a stationary wave?
A. `(2L)/3`
B. `L`
C. `(4L)/3`
D. `2L`
Answer: C
In a pipe that is open at one end and closed at the other, the stationary wave must have:
A node at the closed end.
An antinode at the open end.
These conditions are only satisfied by odd-numbered quarter wavelengths fitting into the pipe:
`L = (nλ) / 4, "where n = 1, 3, 5,..."`
We solve for λ when n = 3 (the second harmonic in a closed pipe):
`L = (3λ)/4 => λ = (4L)/3`
`λ = (4L)/3`
Question 10
A pipe, closed at one end, has a loudspeaker at the open end. For some frequencies of sound from the loudspeaker, a stationary sound wave is formed in the air within the pipe with an antinode at the open end of the pipe. The length of the pipe is 0.85 m.
The length of the pipe is 0.85 m.
The speed of sound in air is 350 m.s-1
Which frequency of sound from the loudspeaker would NOT produce a stationary wave?
A. 100 Hz.
B. 200 Hz.
C. 300 Hz.
D. 500 Hz.
Answer: B
For a pipe closed at one end, stationary waves occur at `L = (nλ)/4, "where n = 1, 3, 5,..."`
The fundamental mode (n = 1) is:
`λ_1 = 4L = 4 xx 0.85 = "3.4 m"`
`f_1 = v / λ = 340 / 3.4 = "100 Hz"`
The allowed harmonic frequencies are `f_n = n xx f_1,"where n is odd: 1, 3, 5,..."`
So the resonant frequencies are:
`f_1 = "100 Hz"`
`f_3 = 3 xx 100 = "300 Hz"`
`f_5 = 5 xx 100 = "500 Hz"`
200 Hz is not an odd multiple of 100 Hz. Hence, the answer is B.
Question 1
A stationary (standing) wave is set up on a vibrating spring. Adjacent nodes are separated by 25 cm. Calculate:
a. The wavelength of the progressive wave.
b. The distance from a node to an adjacent antinode.
Question 2
A string is fixed between points X and Y.
A stationary wave pattern is formed on the stretched string.  The distance between X and Y is 78 cm. The string vibrates at a frequency of 120 Hz. What is the speed of the progressive wave on the string?
The distance between X and Y is 78 cm. The string vibrates at a frequency of 120 Hz. What is the speed of the progressive wave on the string?
Question 3
Find the fundamental frequency and next two possible resonant frequencies for an organ pipe which is 0.17 m long and closed at one end. The speed of sound in air is 340 m.s–1.
Question 4
A vibrating tuning fork of frequency 320 Hz is held over the open end of a resonance tube. The other end of the tube is immersed in water. The length of the air column is gradually increased until resonance first occurs. Taking the speed of sound in air as 340 m.s–1, calculate the length of the air column.
Question 5
A long glass tube is almost completely immersed in a large tank of water. A tuning fork is struck and held just above the open end of the tube as it is slowly raised.
A louder sound is first heard when the height h of the end of the tube above the water is 18.8 cm.
A louder sound is next heard when h is 56.4 cm.
The speed of sound in air is 330 m.s-1. What is the frequency of the sound produced by the tuning fork?
What is the frequency of the sound produced by the tuning fork?
Question 6
A speaker is set up at the open end of a closed tube containing powder.
When the speaker produces sound of frequency 1200 Hz, a stationary wave is produced in the tube.
The powder gathers at the nodes of the stationary wave as shown in the diagram.
The speed of sound in air is 336 m.s-1. What is the value of distance x?
What is the value of distance x?
Question 7
A vertical tube is partially filled with water. A sound wave moves down the tube and is reflected by the surface of the water.
The frequency of the sound wave is gradually increased from zero until a much louder sound is heard. Water is then removed from the tube until a second louder sound is heard.
Water is then removed from the tube until a second louder sound is heard.
Which diagram shows the new pattern of the stationary wave that is formed?
Question 8
The diagram shows part of a stationary wave on a string.
X and Y are points on the string. The vibrations at X and Y are 180° out of phase. What is the distance between X and Y?
What is the distance between X and Y?
A. One-quarter of a wavelength.
B. Half a wavelength.
C. One wavelength.
D. Two wavelengths.
Question 9
A pipe of length L is open at one end and closed at the other. A loudspeaker is at the open end and emits a sound wave into the pipe.
When a stationary wave is formed, there is an antinode at the open end of the pipe.
Which wavelength of sound could be used to produce a stationary wave?
A. `(2L)/3`
B. `L`
C. `(4L)/3`
D. `2L`
Question 10
A pipe, closed at one end, has a loudspeaker at the open end. For some frequencies of sound from the loudspeaker, a stationary sound wave is formed in the air within the pipe with an antinode at the open end of the pipe. The length of the pipe is 0.85 m.
The length of the pipe is 0.85 m.
The speed of sound in air is 350 m.s-1
Which frequency of sound from the loudspeaker would NOT produce a stationary wave?
A. 100 Hz.
B. 200 Hz.
C. 300 Hz.
D. 500 Hz.